技术领域

本发明涉及无线光通信系统中的(N,M)MPPM调制方式基于指数韦伯分布在考虑点误差影响的情况下的采用最佳判决门限和动态判决门限硬解调计算方法，属于无线光通信技术领域。

背景技术

无线光通信，又常常被称作自由空间光通信(Free space opticalcommunication)，即FSO通信。FSO通信是以光波作为载体，在自由空间传输介质中传递通讯信息的一种新型的宽带无线通信手段，它具有成本低廉、架设灵活便捷、抗电磁干扰能力强、保密性好、无需频率资源许可、频带宽等优点，受到了大家的广泛关注。尽管无线光通信有其独特的优势，但是它也受到了诸多因素的影响和制约。在FSO系统中，光束以大气作为传输介质，而大气环境复杂多变，通信链路无疑会受到大气层的干扰。到目前为止，大量研究表明大气湍流是影响通信性能的最主要因素之一，该效应会引起信号在接收端发生振幅和相位的随机抖动，进而导致明显的光强闪烁效应，大大降低了通信系统性能。FSO通信系统除了受到大气湍流这一主要因素的影响，还受到了其它非大气因素的制约。点误差是另一个制约通信质量的主要因素，它是由热膨胀、轻微地震、风速的变化等随机抖动因素造成的发送端和接收端固定平台随机晃动而引起的。而无线光通信系统所采用的光束都较窄，发收两端平台的随机晃动会造成光束的非对准，使得到达接收端的光信号发生随机衰减，进而影响了通信链路性能。为了更好地研究大气衰落对FSO系统的影响，科研人员先后提出了不同的大气信道模型，例如对数正态分布(log-normal,LN)模型(适用于弱湍情况)，K分布模型(适于强湍条件)，以及双伽玛(Gamma-Gamma,GG)分布模型(适用于强、中、弱三湍情况)。其中，GG模型受到了广泛的关注和研究，GG分布模型的数学形式易于处理，并且在使用小孔径接收机时，理论结果能很好的和弱、中、强三种湍流情况下的仿真与实验数据吻合。然而考虑孔径平均效应时，在中到强湍的情况下GG分布模型的结果和实验数据吻合的不是很好。2012年，R.Barrios和F.Dios基于韦伯分布模型，结合激光在湍流中传输的相关性质和孔径平均的物理意义，提出了指数韦伯(exponentiated Weibull,EW)模型。通过和不同孔径大小与不同湍流强度下的仿真和实验数据进行对比，表明该模型能够在任意孔径和任意湍流的情形下描述接收机平面上光强的随机起伏情况。

目前的数字光通信系统大多为强度调制/直接检测(IM/DD)系统，常用的调制方式有开关键控(on-off keying,OOK)和脉冲位置调制(pulse position modulation,PPM)。而新型的多脉冲位置调制(Multipulse Pulse Position Modulation,MPPM)方式，相对于OOK和PPM来说能够提高带宽利用率和功率效率。

硬解调是自由空间光通信系统中一种常用的解调方法，它通过判决门限把受到噪声和衰落影响的信号判定为相应的调制电平。而固定判决门限是其中最简单易得的，但容易产生错误阈值。而最佳判决门限和动态判决门限可以消除这个错误阈值，提高判决的准确度，从而提升系统性能。

目前的问题在于：由于MPPM的复杂性，关于其硬解调特性的报道较少。目前已知硬解调系统算法大多是只考虑大气湍流的作用，而没有考虑点误差的影响。因此，不能用于指导实际的FSO通信系统接收机设计。所以考虑到点误差和EW分布大气湍流的复合作用，基于MPPM调制采用最佳判决门限和动态判决门限进行硬解调判决，计算无线光通信系统的误符号率性能实属当前十分重要的研究方向。

发明内容

考虑点误差和EW分布大气湍流的复合作用，基于MPPM调制采用最佳判决门限和动态判决门限进行硬解调判决，计算无线光通信系统的误符号率性能实属当前十分重要的研究方向。其中，最佳判决门限和动态判决门限硬解调算法都可以消除错误阈值，提高系统判决的正确率。提出的一种误符号率性能估计方法的数学模型，对上述(N,M)MPPM的硬解调算法误符号率进行理论分析，进而正确有效的计算出理论误符号率。

本发明是通过下述技术方案来实现的。

本发明基于EW复合信道模型的MPPM-FSO系统硬解调误符号率计算方法，包括下述步骤：

1)基于指数韦伯EW分布，考虑到点误差的影响，建立点对点的自由空间光通信复合信道模型；

2)根据指数韦伯EW湍流和点误差的复合模型的累积分布模型Fh(h)和概率分布模型fh(h)确定最佳判决门限和动态判决门限的门限值；

3)计算每个时隙在受到指数韦伯EW湍流和点误差复合信道干扰情况下的错误判决的概率；

4)利用高斯拉盖尔多项式，得到误符号率的闭合表达式。

进一步，步骤1)中，基于指数韦伯EW分布，考虑到点误差的影响，建立点对点的自由空间光通信复合信道模型：设x为发送信号序列，y为接收信号序列，则得到信道的数学模型，根据得到的数学模型构建指数韦伯分布模型的概率分布模型和点误差的概率分布模型则可得到大气湍流和点误差的复合信道模型的累积分布模型Fh(h)和概率分布模型fh(h)。

进一步，所述步骤2)中，最佳判决门限的门限值设定利用Matlab通过二分法对下式求未知数yth获得。

进一步，动态判决门限的门限值是检测每一个时隙的信号，取其信号前沿的200ns，根据此时段内检测到的信号强度取设定动态判决门限的值。

进一步，所述步骤3)中，每个时隙在受到指数韦伯EW湍流和点误差复合信道干扰情况下的错误判决，是通过下述方法来实现的：

3a)采用最佳判决门限时，已知复合信道的概率分布模型fh(h)及步骤1)中的数字模型，则可计算出非时隙信号f(y|y0)与时隙信号f(y|y1)抽样值的概率密度函数，进而得到非时隙信号f(y|y0)错误判决的概率，即虚警概率Pf和时隙信号f(y|y1)错误判决的概率，即漏警概率Pm；

3b)采用动态判决门限时，已知(N,M)MPPM信息块中空时隙出现的概率为N-M/N,非空时隙出现的概率为M/N，则每个时隙在仅有高斯白噪声存在的时的误判概率；已知复合信道的概率分布模型及步骤1)中的数学模型，则可计算每个时隙在受到复合信道干扰情况下的错误判决的概率。

进一步，所述步骤4)中，得到误符号率的闭合表达式具体包括：

4a)采用最佳判决门限时，对于(N,M)MPPM，根据正确解调的概率Pc＝(1-Pm)M(1-Pf)N-M,得到误符号率；

4b)采用动态判决门限时，对于(N,M)MPPM，正确解调的概率为Pc＝(1-SLER)N，得到误符号率。

本发明具有以下优点：

本发明中首先提出了一种基于EW复合信道模型的MPPM-FSO系统硬解调误符号率计算方法，该方法复杂度低，误符号率系统性能上优于其他硬解调算法；

本发明方法中的复合信道模型相较于单一的大气湍流模型考虑了点误差对系统性能的影响，更为符合实际情况。

附图说明

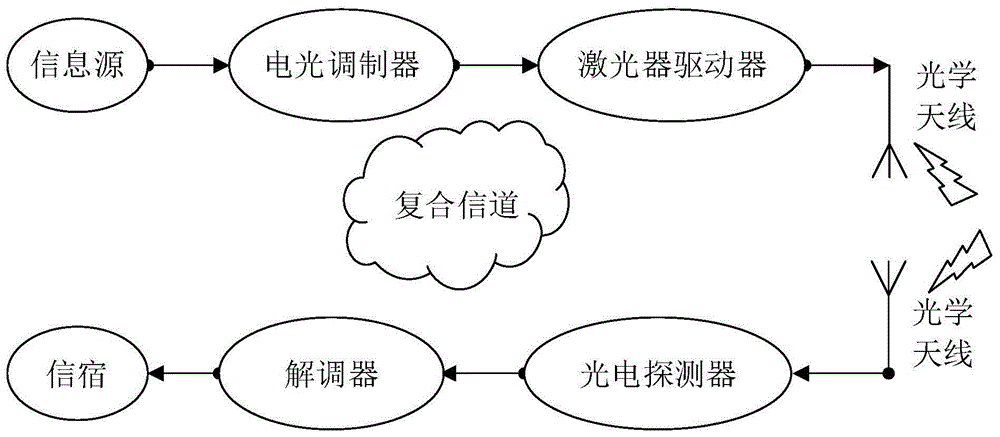
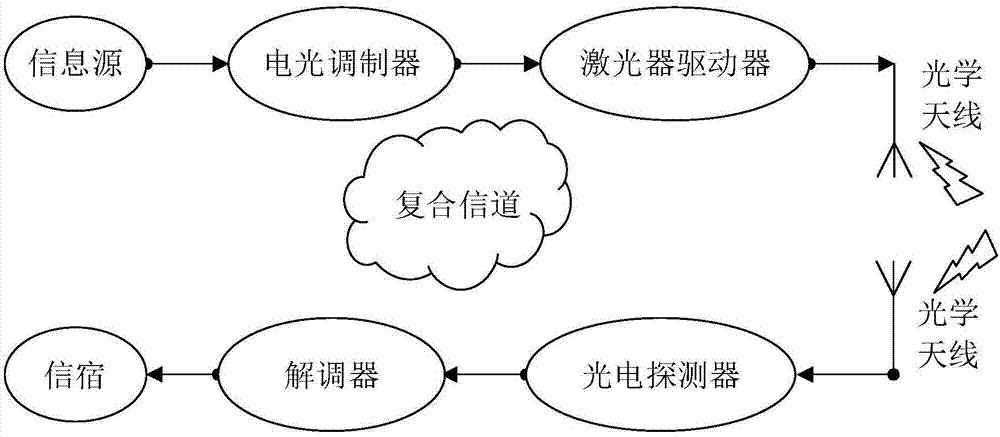
图1是复合信道下MPPM调制解调系统模型；

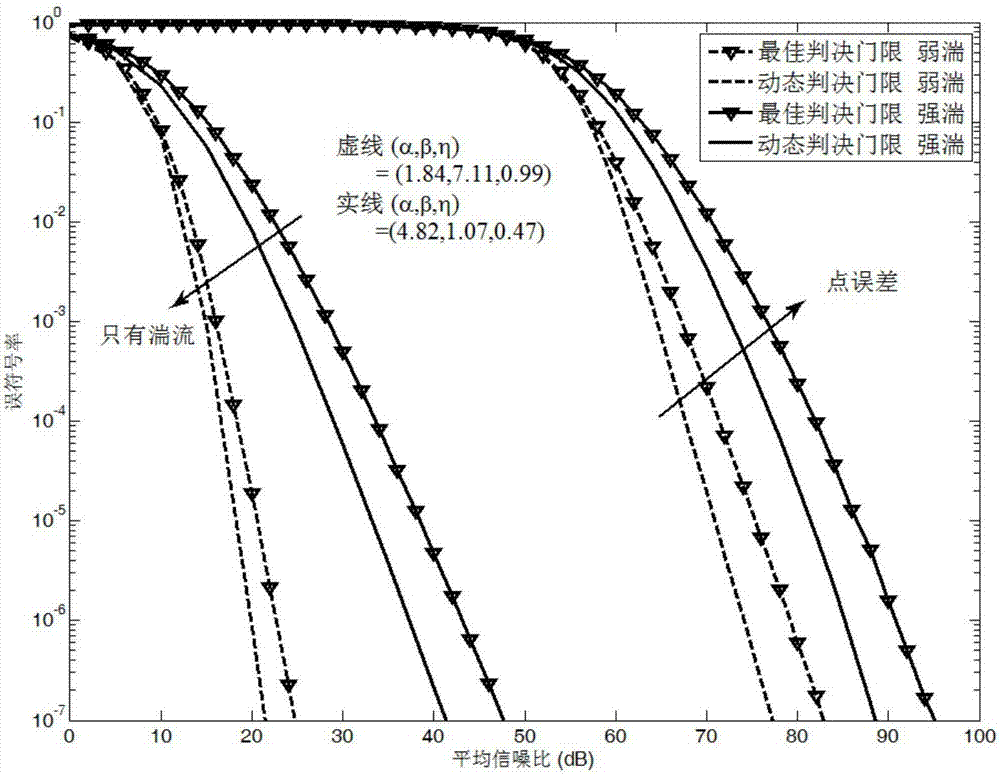
图2是强湍和弱湍流两种情况下，考虑点误差和不考虑点误差的误符号率对比图；

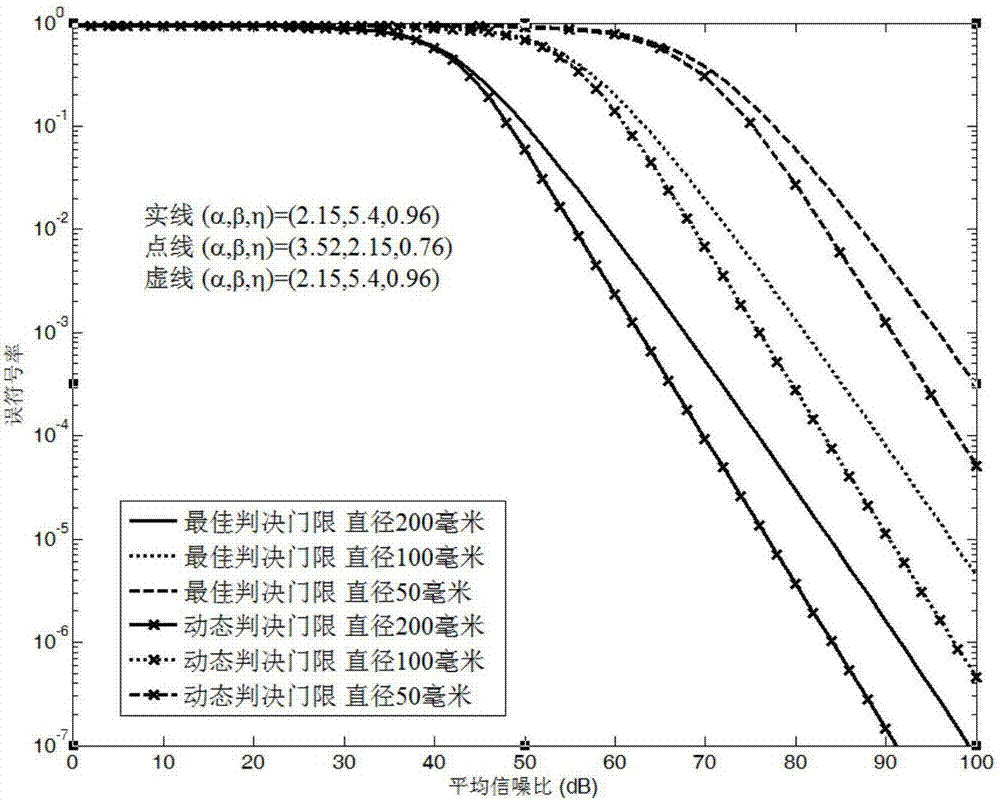
图3是中湍情况下，孔径直径变化时的误符号率理论值对比图；

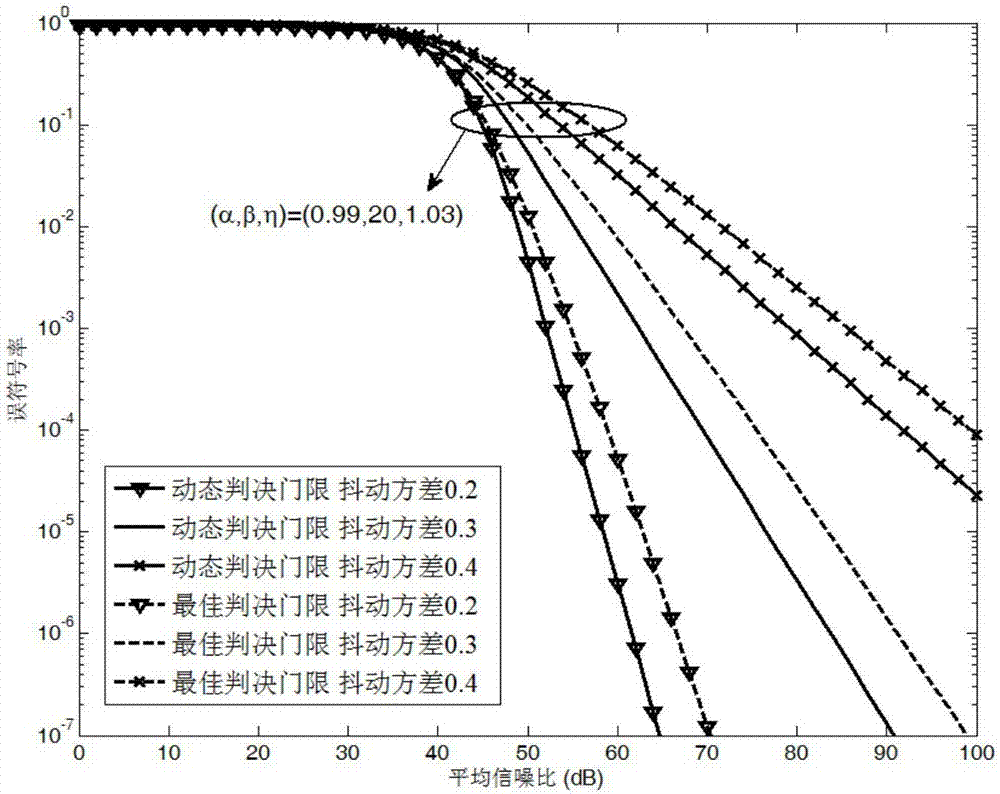
图4是弱湍流情况下，抖动方差变化时的误符号率理论值对比图；

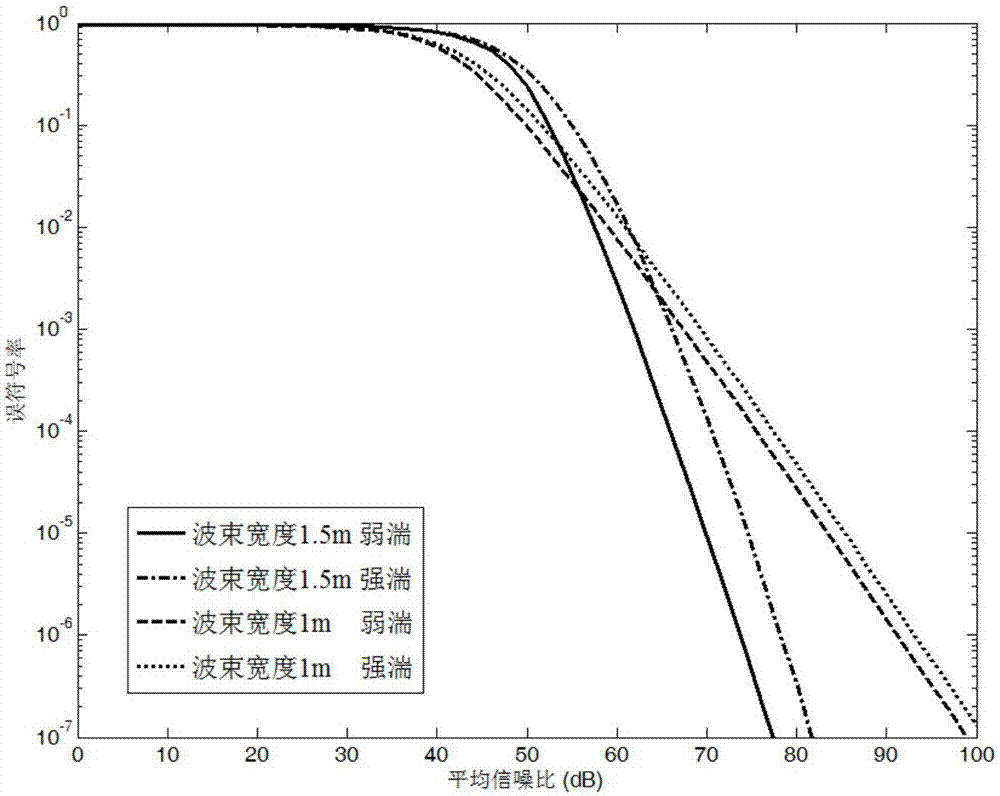
图5是在强湍和弱湍流两种情况下采用最佳判决门限方案，波束宽度变化时的误符号率理论值对比图；

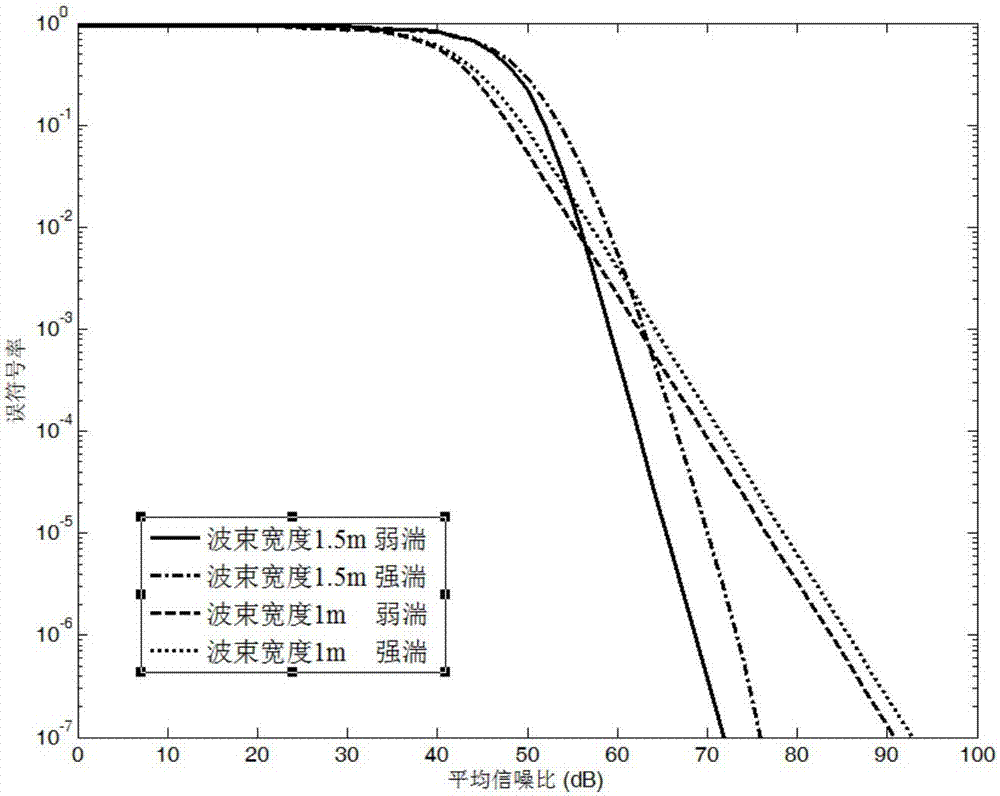
图6是在强湍和弱湍流两种情况下采用动态判决门方案，波束宽度变化时的误符号率理论值对比图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面结合附图和具体实施方式进一步详细说明。本实施例仅表示对本发明的原理性说明，不代表对本发明的任何限制。

本发明基于MPPM调制采用两种判决门限的硬解调误码率计算方法，包括：

步骤1基于指数韦伯EW分布，考虑到点误差的影响，建立点对点的自由空间光通信复合信道模型

1a)设x为发送信号序列，y为接收信号序列，则信道的数学模型为：

y＝Rhx+n

其中，n表示均值为0、方差为的加性高斯白噪声。R为光电探测器响应率，h为服从指数韦伯EW复合信道分布的信道衰落，h＝hahp；其中，ha为服从EW分布的信道衰落，hp为点误差损失因数。

1b)根据步骤1a)得到的数学模型构建指数韦伯EW分布模型的概率分布模型和点误差的概率分布模型表示为

其中，ha为服从指数韦伯EW分布的信道衰落，hp为点误差损失因数；β为形状参数，β＞0，其取值与闪烁指数相关；α为给定观测空间内，准直传播的光束与非准直传播的光束被成功接收的平均量，α＞0；η尺度参数，η＞0；γ为等效波束宽度和抖动标准差的比值，γ＝wzeq/2σs；其中wzeq为等效波束宽度，σs为抖动标准差；A0为当探测器与波束中心之间的偏移量为0时接收机接收到的光强，A0＝[erf(v)]2，其中ν为孔径和距离z处的波束宽度的比值，其中a为探测器的孔径半径，wz为距离发射端z处的波束宽度。

1c)根据这两个式子则可推导出指数韦伯EW复合信道的累积分布模型Fh(h)和概率分布模型fh(h)为：

式中，Γ(a,x)为上伽马不完全函数，为梅耶尔G函数；j为求和符号的计数器。

步骤2根据指数韦伯EW湍流和点误差的复合信道模型的累积分布模型Fh(h)和概率分布模型fh(h)确定最佳判决门限和动态判决门限的门限值

2a)最佳判决门限的门限值可利用Matlab通过二分法对下面式子求未知数yth获得

式中，N为MPPM调制的一个信息块所包含的时隙个数，M为此N个时隙个数中的脉冲个数；t为被积函数的积分变量；yth为门限值；μ为系数，而μ2＝(RNPt/M)2，R为光电转换效率，Pt为发射端的平均发射功率；g为信噪比；exp(·)为以自然数e为底的指数函数；Γ(·)为伽马函数；erf(·)为误差函数；erfc(·)为余弦误差函数；j为求和符号的计数器。

2b)动态判决门限是检测每一个时隙的信号，取其信号前沿的200ns，根据此时段内检测到的信号强度取设定动态判决门限的值。经过对前沿值的检测，再进行判决门限的设定相当于没有了湍流的影响，影响最终判决的只有高斯白噪声。

步骤3计算每个时隙在受到指数韦伯EW湍流和点误差复合信道干扰情况下的错误判决的概率

3a)采用最佳判决门限时，已知复合信道的概率分布模型fh(h)及步骤1)中的数学模型，则可计算受到指数韦伯EW湍流和点误差干扰情况下出非时隙信号f(y|y0)与时隙信号f(y|y1)抽样值的概率密度函数分别为：

式中，σn2为加性高斯白噪声的方差；f(y|y1)为有信号时隙抽样值的概率密度函数，f(y|y0)为非信号时隙抽样值的概率密度函数；

虚警概率Pf即将非时隙信号错误判决的概率，为：

漏警概率Pm即将时隙信号错误判决的概率，为：

3b)采用动态判决门限时，已知(N,M)MPPM信息块中空时隙出现的概率为N-M/N,非空时隙出现的概率为M/N，则每个时隙在仅有高斯白噪声存在的时的误判概率为

已知复合信道的概率分布模型fh(h)及步骤1)中的数字模型，则可计算每个时隙在受到复合信道干扰情况下的错误判决的概率，

步骤4利用高斯拉盖尔多项式，得到误符号率的闭合表达式

4a)采用最佳判决门限时，对于(N,M)MPPM，正确解调的概率为Pc＝(1-Pm)M(1-Pf)N-M，其中脉冲时隙和非脉冲时隙正确的概率为

则误符号率为

式中，Hi是广义拉盖尔公式中的权重；xi为广义高斯拉盖尔多项式的第i个根；k是广义高斯拉盖尔多项式的总项数。

4b)采用动态判决门限时，对于(N,M)MPPM，正确解调的概率为Pc＝(1-SLER)N，则误符号率为

本发明的正确性和优点可通过以下理论结果对比进一步说明：

通过MATLAB进行解析计算，首先，准确描述所推导的公式；然后，比较有点误差和没有点误差的情况；其次，比较最佳判决门限和动态判决门限的性能；最后，改变其中各种变量的值。

理论结果

图1给出在指数韦伯EW湍流和点误差的复合信道下，采用MPPM调制并解调的无线光通信系统模型。图2给出在强湍和弱湍条件下采用最佳判决门限和动态判决门限方案，考虑点误差和不考虑点误差两种情况下的误符号率随信噪比变化的对比图，可以看出，考虑点误差比不考虑点误差情况下误码率性能明显下降。图3给出在中湍情况下采用最佳判决门限和动态判决门限方案，孔径直径变化时的误符号率随信噪比变化的对比图。可以看出，随着接收孔径的增大，两种判决门限的误符号率都有明显下降，通信性能提高。图4给出在弱湍情况下采用最佳判决门限和动态判决门限方案，抖动方差变化时的误符号率随信噪比变化的对比图。可以看出，随着抖动方差的减小，两种判决门限的误符号率都有明显下降，性能提高。图5、6给出在强湍和弱湍条件下分别采用最佳判决门限和动态判决门限方案，波束宽度变化时的误符号率随信噪比变化的对比图。可以看出,在低信噪比的时候波束宽度越窄性能越好，在高信噪比的时候波束宽度越宽性能越好。因为当信噪比比较小时，系统的误符号率主要受发送功率的影响，波束宽度越窄，收集到的光功率越大，系统的误符号率性能就越好。而当信噪比增大到一定值时，系统误符号率主要受瞄准误差的影响。此时，宽的波束宽度到达接收端的光斑面积要大于窄的波束宽度，即接收到的光强要大，则系统的误符号率就越低。

本发明并不局限于上述实施例，在本发明公开的技术方案的基础上，本领域的技术人员根据所公开的技术内容，不需要创造性的劳动就可以对其中的一些技术特征作出一些替换和变形，这些替换和变形均在本发明的保护范围内。