技术领域

本发明属于近场动力学和冲击问题领域，具体涉及一种基于近场动力学键基理论对冰雹冲击飞机复合材料层合板结构损伤行为的研究。

背景技术

复合材料与单一材料相比具有更高的比刚度和比模量，在强度刚度、抗疲劳及可设计性等方面具有显著优势被广泛应用于工程结构之中，尤其在航空航天领域。在服役阶段，飞机上的复合材料结构比如说机翼前缘和雷达罩等，通常可能会受到冰雹的高速冲击而损伤。为了保证和提高飞机复合材料层合板结构的设计性和使用安全性，研究冰雹冲击下飞机复合材料结构动态损伤行为就显得尤为重要。针对这类冲击问题，传统的有限元方法无法准确地模拟冰雹冲击过程中大尺度变形，并且无法在不连续处对位移求导，而近场动力学方法能够很好地解决该问题。

近场动力学是一种通过求解空间积分微分方程来描述材料力学行为的非局部无网格方法。避免了基于连续性假设建模和求解空间微分方程的传统宏观方法在面临不连续问题时的奇异性，又突破了经典分子动力学方法在计算尺度上的局限，在宏/微观不连续力学问题分析中均表现出很高的求解精度和效率。

发明内容

要解决的技术问题

为了避免传统的有限元方法无法准确地模拟冰雹冲击过程中大尺度变形，并且无法在不连续处对位移求导，本发明提出一种基于近场动力学对冰雹冲击飞机复合材料层合板的建模方法。

技术方案

本发明基于近场动力学理论，引入了纤维键、基体键、层间法向键和层间剪切键四种键模拟冲击过程中的破坏，基于双材料界面模型，建立可以描述不同材料冲击作用的键常数表达式。建立了近场动力学模型，并且用数值分析方法考虑了复合材料层合板的损伤演化规律和动态力学性能，揭示了在冰雹的高速冲击下复合材料层合板结构受力时的破坏机理及影响因素。

一种基于近场动力学对冰雹冲击飞机复合材料层合板的建模方法，其特征在于步骤如下：

步骤1：建立冰雹冲击复合材料层合板近场动力学仿真模型，所述的仿真模型包括冰雹和复合材料层合板；仿真模型涉及的参数包括冰雹的直径D、密度ρ1；复合材料层合板的尺寸、材料参数；所述的复合材料层合板的尺寸：长为L、宽为W、厚为C、单层厚度为T；

步骤2：对仿真模型施加边界条件并进行离散化

对复合材料层合板施加边界条件：将复合材料层合板进行四面固支，固支厚度为h；将复合材料层合板均匀离散成体积一样的晶格，即物质点；设定物质点键长Δx，冰雹与复合材料层合板之间初始距离为根据物质点间距d确定层合板模型中物质点的数量：再根据邻域半径δ构建所有物质点的邻域矩阵；赋予冰雹初始冲击速度为v0；

利用冰雹的直径、密度和速度来表征冰雹的动能

步骤3：构造冰雹-层合板键函数及引入四种键

基于双材料界面模型，建立冰-层合板界面键的键常数表达式：

其中：c为界面串联键的键常数，cA为复合材料层合板基体键的键常数，cB为冰雹的键常数，键A和B的长度分别为lA和lB，组合键总长为l＝lA+lB；

引入权函数和表示各键长度与总长的比，以简化上述键常数的表达式：

在层合板模型中，引入四种键来模拟冲击过程中三种破坏形式，所述的四种键为纤维键、基体键、层间法向键和层间剪切键，所述的三种破坏形式为剪切、拉伸和压缩破坏，并给出了四种键型的临界伸长率：

sft＝Xt/E1(s≥0)

sfc＝Xc/E1(s<0)

smt＝Yt/E2(s≥0)

smc＝Yc/E2(s<0)

其中：sft为纤维键在拉伸情况下的临界伸长率，sfc为纤维键在压缩情况下的临界伸长率；smt为基体键在拉伸情况下的临界伸长率，smc为基体键在压缩情况下的临界伸长率；Xt为复合材料在纤维上的拉伸强度；Xc为复合材料在垂直于纤维方向上压缩强度；Yt为复合材料在纤维方向上的拉伸强度；Yc为复合材料在垂直于纤维方向上的压缩强度；s0N为层间法向键的临界伸长率；为层间剪切键的临界剪切角；GIIC＝0.75GIC；在实际计算中可以认为C为板厚度；Em为层间弹性模量；Gm为层间剪切模量；E1为纵向弹性模量，E2为横向弹性模量；

用上述临界伸长率表征层合板内键的破坏情况；

步骤4：迭代求解

基于复合材料层合板近场动力学理论，对仿真模型进行迭代，求解每一时间步物质点的位置和位移，第n层中的位置k质点的运动方程为：

式中：是材料密度，为层合板物质点速度，为力密度矢量，和分别代表质点和的体积；

计算物质点间的伸长率：

式中，η＝u(x′,t)-u(x,t)物质点的相对位移，ξ＝x′-x为为物质点的相对位置，μ(η,ξ,t)为键的损伤函数，公式如下：

当s超过临界值s0，所述的临界值s0为纤维键、基体键、层间法向键和层间剪切键中任意一种键的临界伸长率时，该键断裂失效，键力随即消失，两物质点间不再相互作用；

计算界面键的键力函数：

以连接键的破坏情况占比来表示各物质点邻域矩阵内局部破坏水平：

其中，0表示完整状态，而1表示完全损伤状态，即时，层合板物质点领域内所有的界面拉伸键和界面剪切键全部断裂；0～1之间的数值，即为局部损伤程度的量化表征。

优选地：所述的复合材料层合板为CCF300/10128H。

优选地：所述的复合材料层合板的材料参数如下表所示：

层合板材料性能参数

优选地：所述的复合材料层合板的铺层有以下三种：单向铺层[0°]8，反对称正交铺层[0°/90°]2S和准各向同性铺层[0°/45°/90°/-45°]S。

优选地：所述的固支厚度为h为3mm，物质点键长Δx为1mm，冰雹与层合板之间初始距离为0.5mm，冰雹初始冲击速度为v0为100m/s，物质点间距d为1mm，邻域半径δ为3.015mm。

有益效果

本发明提出的一种基于近场动力学对冰雹冲击飞机复合材料层合板的建模方法，采用了近场动力学方法对冰雹冲击飞机复合材料层合板结构进行建模，相比于基于传统连续介质力学理论的有限元方法，近场动力学理论采用积分方程重新构造了复合材料层合板的微分动力学方程，从而避免了不连续问题中导数不存在的问题。因此，近场动力学方法可以模拟出冲击过程中，复合材料层合板裂纹的萌生与扩展。

基于权函数构造了双材料键串联的冰-层合板界面模型，该模型能反映界面处材料的力学性能。引入四种键(纤维键、基体键、层间法向键和层间剪切键)来模拟冲击过程中三种主要的破坏形式(剪切、拉伸和压缩破坏)，并给出了四种键型的断裂准则和临界伸长率，键的临界伸长率取代了传统连续介质力学方法中的强度理论反映材料的损伤。

本发明建立了一种改进的纤维增强复合材料层合板动力学模型，对复合材料层合板受到冰雹冲击作用下的动态损伤过程进行分析，进而对飞机结构冰雹防撞设计以及损伤检测具有一定的指导意义。

1、发现冲击过程中复合材料层合板的破坏主要以基体键和层间键为主，力密度图显示冲击过程中冲击位置所在的纤维方向力密度要明显大于其它位置，表明纤维键对复合材料的抗冲击能力有明显的增强作用，因此在复合材料层合板优化设计中，可以通过增加复合材料层合板的纤维提升其抵抗冲击的能力。

2、对三种铺层方案下复合材料层合板的抗冰雹冲击性能进行比较发现：准各向同性铺层>反对称正交铺层方案>单向铺层。在优化设计中，可以通过改变层合板的铺层角度和铺层顺序改善层合板的抗冲击能力，进而提高飞机的抗冲击性能。

附图说明

附图仅用于示出具体实施例的目的，而并不认为是对本发明的限制，在整个附图中，相同的参考符号表示相同的部件。

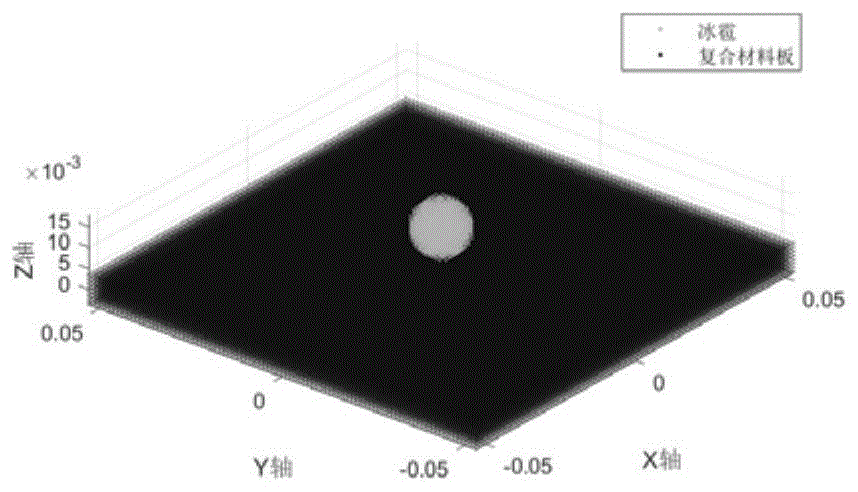
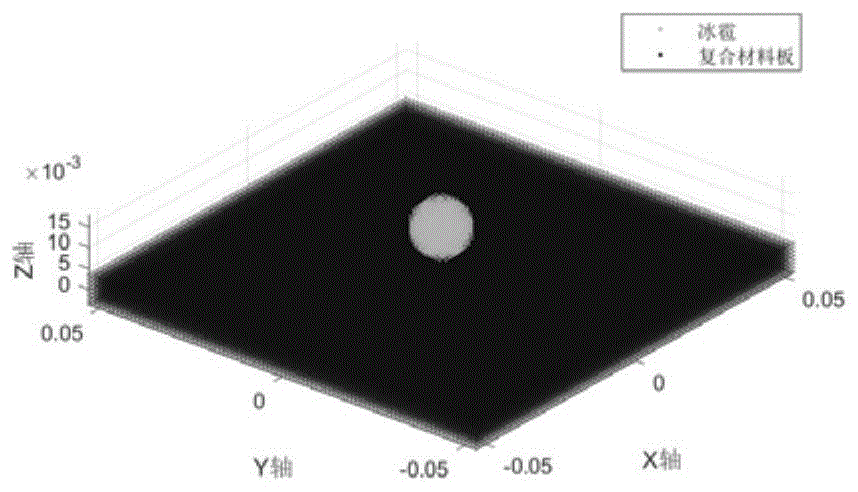
图1是冰雹冲击复合材料层合板示意图。

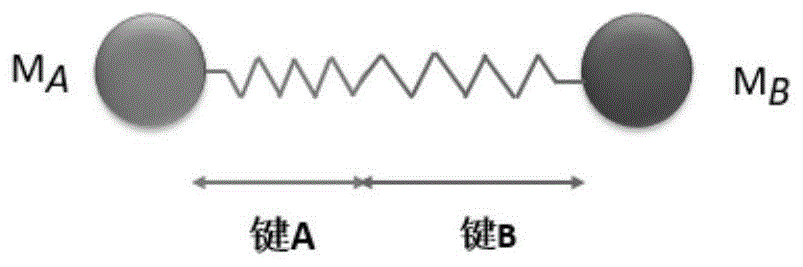
图2是两种材料间键的串联模型。

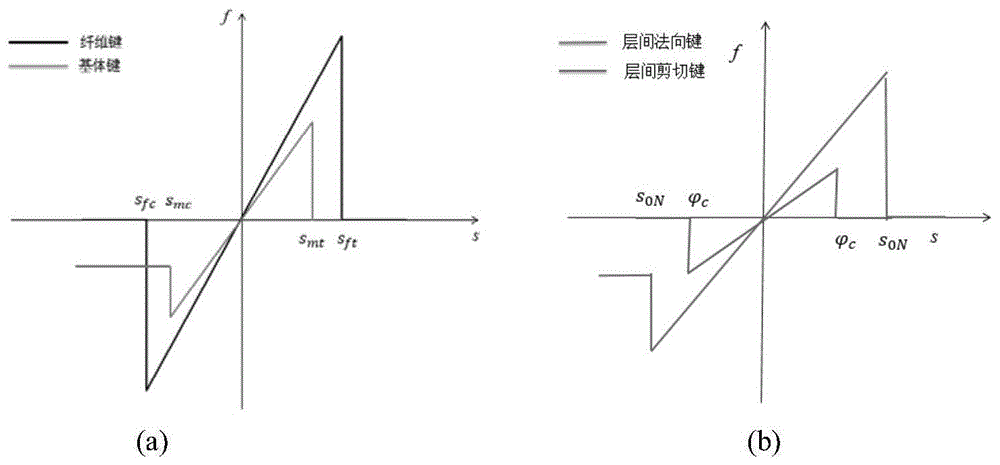
图3是键力f随伸长率s的变化：(a)纤维键与基体键(b)层间法向键与层间剪切键。

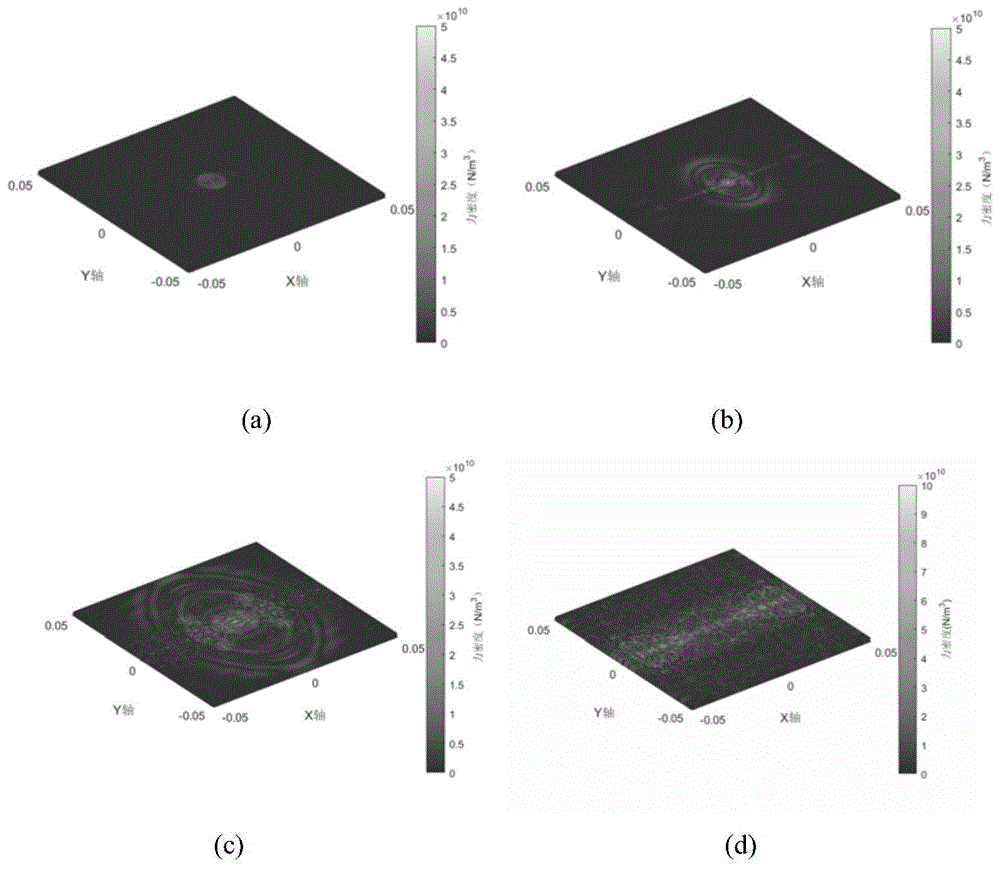
图4是冲击过程上层板力密度变化图：(a)t＝1×10-5s(b)t＝2×10-5s(c)t＝4×10-5s(d)t＝1×10-4s。

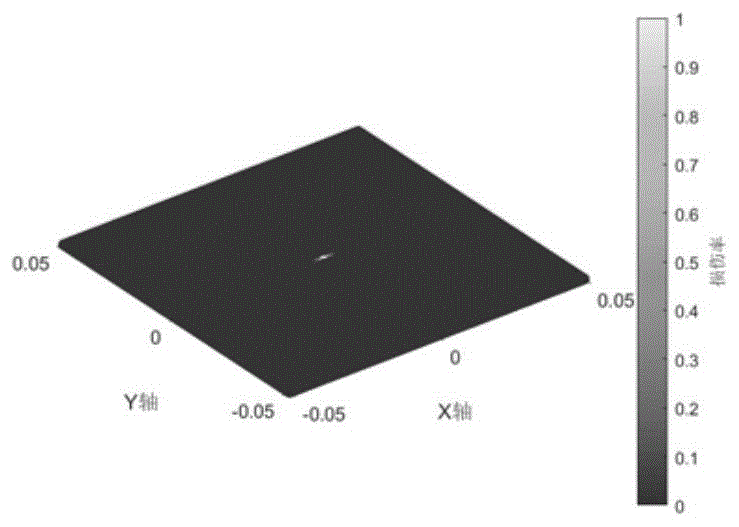
图5是冲击过程上层板纤维键最终损伤率示意图。

图6是冲击过程上层板基体键最终损伤率示意图。

图7是冲击过程上层板层间键最终损伤率示意图。

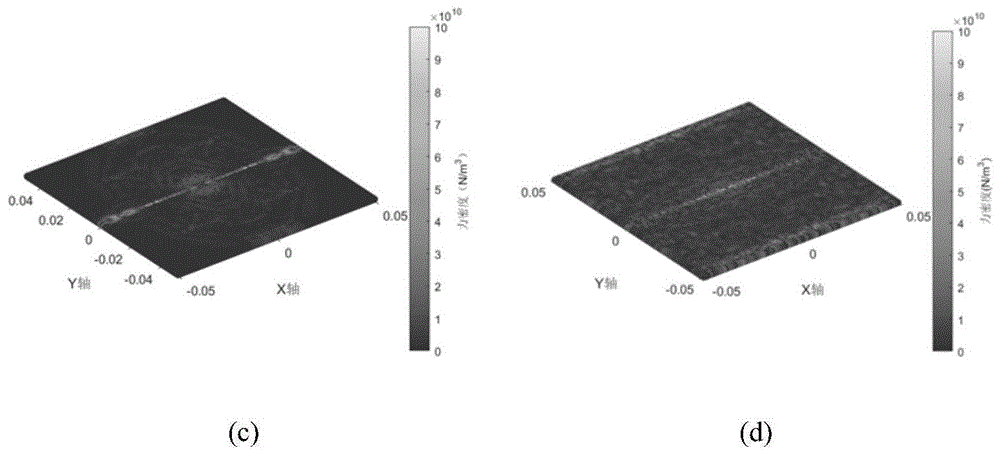
图8是冲击过程下层板力密度变化图：(a)t＝1×10-5s(b)t＝2×10-5s(c)t＝4×10-5s(d)t＝1×10-4s。

图9是冲击过程下层板基体键最终损伤率示意图。

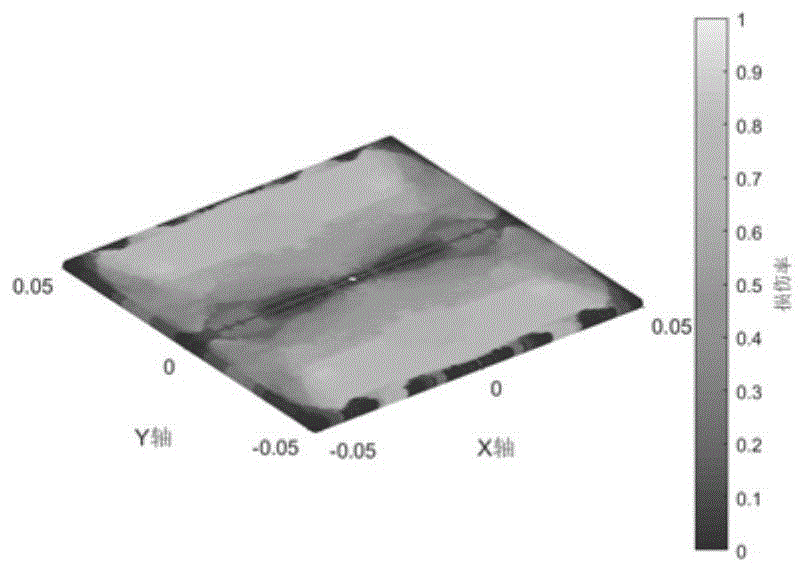
图10是冲击过程下层板层间键最终损伤率示意图。

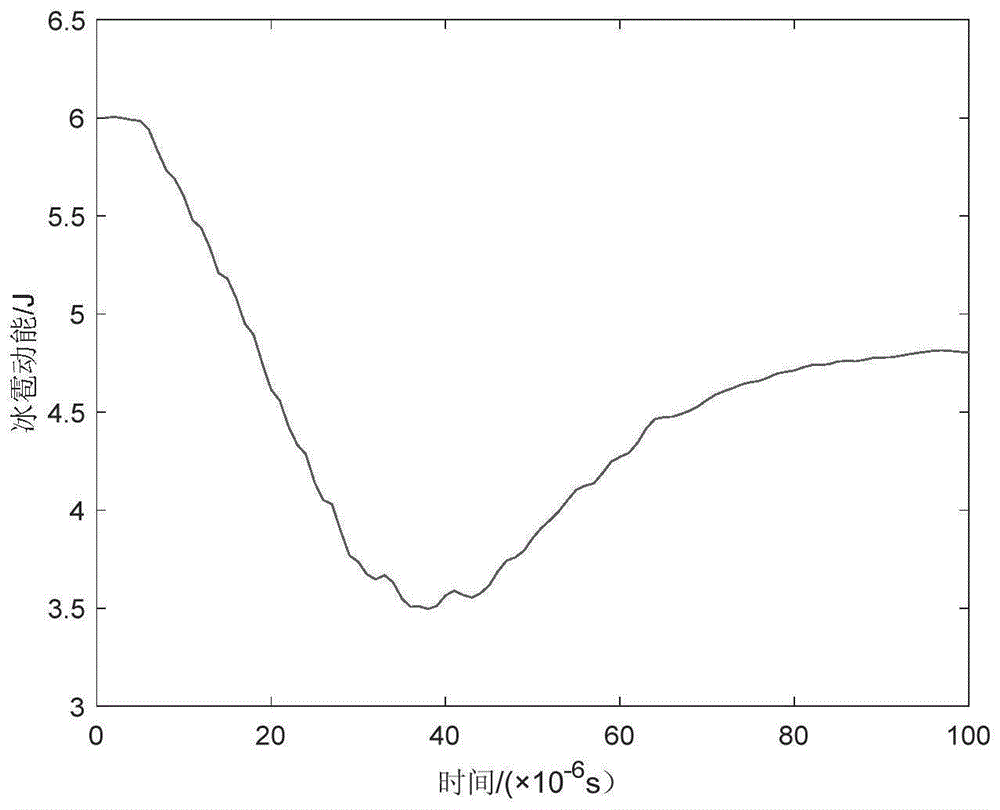
图11是冲击过程中冰雹的动能变化图。

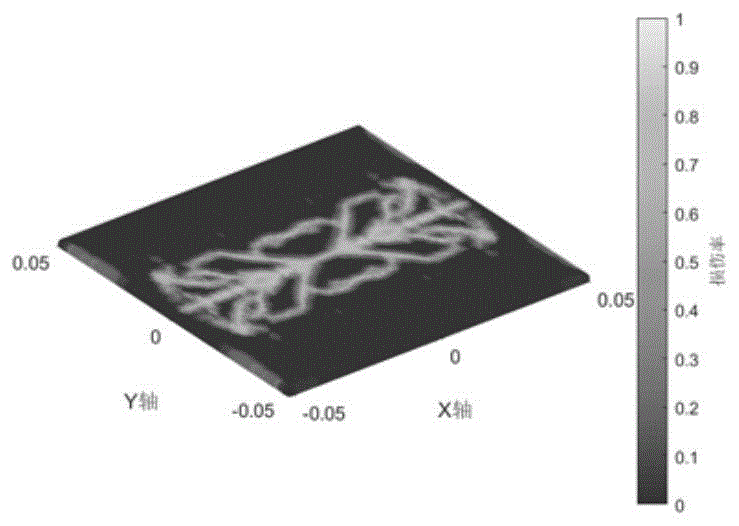
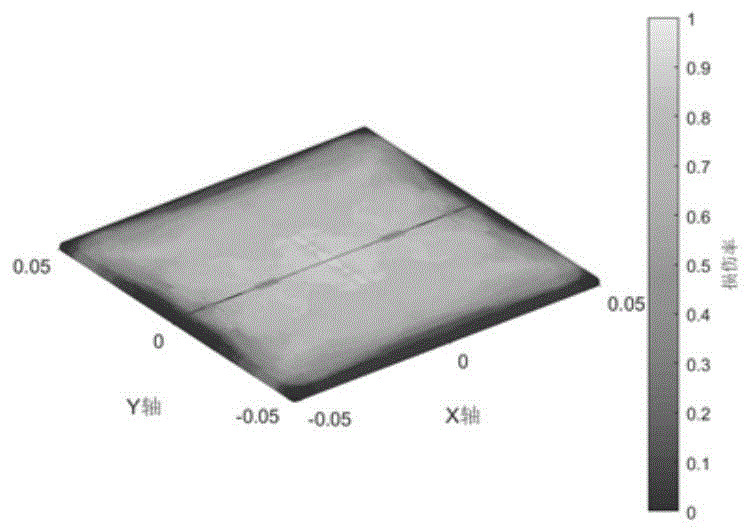
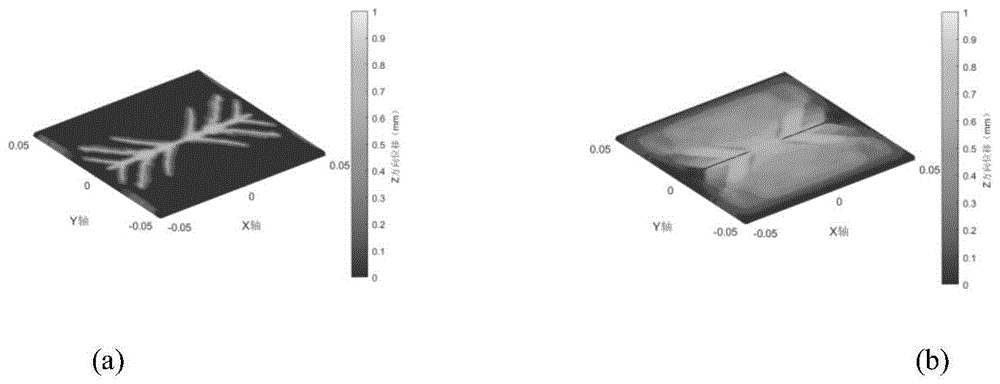
图12单向铺层[0°]8下层板损伤：(a)基体键(b)层间键。

图13反对称正交铺层[0°/90°]2S下层板损伤：(a)基体键(b)层间键。

图14准各向同性铺层[0°/45°/90°/-45°]S下层板损伤：(a)基体键(b)层间键。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图和实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。此外，下面描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

第一步：建立冰雹近场动力学仿真模型，冰雹的直径D取15mm，冰雹的密度为846kg·m-3；

建立层合板近场动力学仿真模型，层合板长L＝101mm，宽W＝101mm，厚为C＝8mm,单层厚度为T＝1mm，共8层，层合板的材料参数如表1所示。铺层方案有以下三种：单向铺层[0°]8，反对称正交铺层[0°/90°]2S和准各向同性铺层[0°/45°/90°/-45°]S，本实施例采用反对称正交铺层[0°/90°]2S，(其中，“[]”内的数字表示铺层角度的排列顺序，下标2表示按此顺序再重复铺放一次，下标S表示在此基础上按之前顺序的倒序重复铺放)。

表1层合板材料性能参数

复合材料结构具有各向异性，其力密度矢量t(k)(j)可以写成如下形式：

式中：

t(k)(j)为近场域内的物质点j对物质点k的相互作用，u(j)为物质点j的位移，x(j)、x(k)为变形前后层合板物质点的横坐标，t为某时刻，A(k)(j)和B(j)(k)是辅助参数。

第n层中的位置k质点的运动方程为：

式中：是材料密度，为层合板物质点速度，为力密度矢量，和分别代表质点和的体积

第二步：将层合板均匀离散成体积一样的晶格，即物质点；根据物质点间距d确定层合板模型中物质点的数量：模型中物质点的数量为N为91304个；再根据邻域半径δ构建所有物质点的邻域矩阵；计算时间步长取0.2μs，计算步数取1000步；

对层合板施加边界条件：将层合板进行四面固支，固支厚度为3mm。物质点键长Δx＝1mm，物质点体积ΔV＝1.0×10-3mm3，冰雹与层合板之间初始距离为赋予冰雹初始冲击速度为v0＝100m/s，冰雹的动能冲击初始冰雹与板的位置示意图如图1所示。

第三步：为了将冰雹模型和复合材料层合板模型纳入统一的计算框架，基于双材料界面模型，建立冰雹-层合板界面键的键常数表达式。假设两个不同材料性质的物质点间的短程力作用键为一个组合串联键，键A代表复合材料层合板基体键，键B则代表冰雹内的键，如图2所示。

在初始状态下，键A和B的长度分别为lA和lB，组合键总长为l＝lA+lB。变形后键A和B的伸长率分别为sA和sB，组合键总伸长率为s＝sA+sB。串联模型中，静力平衡状态下两键A和B内力相等，csh表示组合串联键的整体键常数：

fsh＝cshs＝cAsA＝cBsB (4)

根据以上关系以及伸长率的定义sA＝ΔlA/lA、sB＝ΔlB/lB和s＝(ΔlA+ΔlB)/l(其中Δl表示相应键的伸长量)可得：

引入权函数和表示各键长度与总长的比，以简化上述键常数的表达式：

为了能将两种材料纳入统一计算框架，所以设置lA＝lB，所以ωA＝ωB＝0.5，

在层合板模型中，引入四种键(纤维键、基体键、层间法向键和层间剪切键)来模拟冲击过程中三种主要的破坏形式(剪切、拉伸和压缩破坏)，并给出了四种键型的断裂准则和临界伸长率；

假设与纤维方向夹角小于10°的键均为纤维键，而夹角大于10°的键为基体键。层间法向键和层间剪切键的性能不受单层板的铺设角度影响。由于K-PD模型的作用，键的长度越短，对物质点的作用越强。在拉伸和压缩载荷作用下，当键的伸长率达到临界值时，纤维键会立即破坏，并完全失去承载能力。基体键在拉伸载荷下失效机理和纤维键相同，但对于压缩载荷则略有不同。在压缩作用下当基体键的伸长率达到临界伸长率时，基体键虽然也会受到一定程度的破坏，但仍能承受一半的屈服载荷。键的破坏过程不可逆的。层间法向键类似于基体键，在拉伸载荷作用下当层间法向键的伸长率超过临界伸长率，键就会立刻破坏并完全失效，在压缩载荷作用下键的伸长率超过临界伸长率，层间法向键虽然也会发生一定破坏，但是仍能承受屈服时一半的载荷大小。对于层间剪切键，类似于纤维键，当键的夹角超过临界剪切角时，临界剪切键会完全破坏，失去承载能力。层间法向键类似于基体键，在拉伸载荷作用下当层间法向键的伸长率超过临界伸长率，键就会立刻破坏并完全失效，在压缩载荷作用下键的伸长率超过临界伸长率，层间法向键虽然也会发生一定破坏，但是仍能承受屈服时一半的载荷大小。对于层间剪切键，类似于纤维键，当键的夹角超过临界剪切角时，临界剪切键会完全破坏，失去承载能力。图3给出了键力f随伸长率s的变化。

图中，sft为纤维键在拉伸情况下的临界伸长率，sfc为纤维键在压缩情况下的临界伸长率；smt为基体键在拉伸情况下的临界伸长率，smc为基体键在压缩情况下的临界伸长率；s0N是层间法向键的临界伸长率，是层间剪切键的临界剪切角。

利用以下公式求解层合板面内键的临界伸长参数：

对于纤维键：

sft＝Xt/E1(s≥0) (7)

sfc＝Xc/E1(s<0) (8)

对于基体键：

smt＝Yt/E2(s≥0) (9)

smc＝Yc/E2(s<0) (10)式中：

Xt——复合材料在纤维上的拉伸强度；

Xc——复合材料在垂直于纤维方向上压缩强度；

Yt——复合材料在纤维方向上的拉伸强度；

Yc——复合材料在垂直于纤维方向上的压缩强度。

基体键控制平面内所有方向的材料属性，具有各向同性的性质，所以基体键的临界伸长率可以使用二维平面情况下各向同性材料的临界伸长率的形式。纤维键主要负责纤维增强方向的材料性能，其临界伸长率取决于纤维断裂所需的断裂能。层间法向键和层间剪切键的临界变形量可以通过层间能量释放率求得。令相邻层物质点的层间法向键和层间剪切键断裂，计算断裂所需能量，并令其与对应类型裂纹能量释放率相等，可以得到层间法向键的临界伸长率s0N和层间剪切键的临界剪切角表达式如下：

一般认为GIIC＝0.75GIC，在实际计算中可以认为板厚度C为8mm，Em为层间弹性模量，Gm为层间剪切模量。

第四步：对所述冰雹冲击复合材料层合板近场动力学模型迭代求解，对公式3时域积分得到层合板质点位移和位置。

计算物质点间的伸长率：

式中，η＝u(x′,t)-u(x,t)物质点的相对位移，ξ＝x′-x为物质点的相对位置，μ(η,ξ,t)为键的损伤函数，公式如下：

当s超过临界值s0，即公式7-12表示的任意一种临界伸长率时，该键断裂失效，键力随即消失，两物质点间不再相互作用。

计算界面键的键力函数：

以连接键的破坏情况占比来表示各物质点邻域矩阵内局部破坏水平：

其中，0表示完整状态，而1表示完全损伤状态，即时，层合板物质点领域内所有的界面拉伸键和界面剪切键全部断裂。0～1之间的数值，即为局部损伤程度的量化表征。

最后输出结果并进行可视化，据此实现了冰雹冲击复合材料层合板结构的近场动力学仿真。从图4到图10可以看出，冰雹冲击复合材料层合板过程中层合板的破坏主要以基体键和层间键为主，这和实验过程中层合板的失效形式主要为基体开裂和分层失效结果相吻合。从力密度云图中可以看出，冲击过程中冲击位置所在的纤维方向力密度要明显大于其它位置，因此得出，纤维键对复合材料的抗冲击能力有明显的增强作用。

从图11可以看到，冰雹在接触到复合材料层合板后，由于初期接触面积相当小，冰雹整体的动能减小幅度较小，随后随着冲击面积的逐渐增大，冰雹的动能迅速减小；当动能降到最低点，由能量守恒可知，冰雹此时内部的内能最大，能量集中在冰雹核心处；随后冰雹上半部逐渐开始破坏，出现裂纹，破碎粒子反弹，使冰雹的总动能迅速增加；最后冰雹完全破坏，冰雹粒子的总动能趋于稳定。

从图12-14可以看到，单层铺层方案的损伤图案比较单调，基体键和层间键的损伤扩展方向均呈现沿与纤维方向成45°夹角的方向扩展。基体键的损伤在下层板呈现为沿纤维方向的条状，并沿与纤维方向成45°夹角的方向不断分叉扩展，最后沿垂直于纤维方向的轴线呈现对称的树状。层间键的损伤沿垂直于纤维方向成扇形向两端扩散，高损伤率区域呈现为垂直于纤维方向的蝴蝶状。反对称正交铺层的基体损伤图案最为复杂，层间键的损伤面积最大；准各向同性铺层的基体损伤与反对称铺层有一定的相似性，但垂直于纤维方向的基体损伤路径纹路要稀疏一些，层间键损伤区域呈现圆形，且在纤维方向两端出现对称花瓣状损伤严重区域。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明公开的技术范围内，可轻易想到各种等效的修改或替换，这些修改或替换都应涵盖在本发明的保护范围之内。