技术领域

本发明属于近场动力学和冲击问题领域，具体涉及一种基于近场动力学理论的飞机电脉冲除冰模拟方法。

背景技术

随着多电飞机和全电飞机的不断发展，取消飞机发动机的引气的新型的设计使得飞机绝大部分结构的防除冰装置需依赖电力驱动。比如在波音787在机翼中安装了电热除冰系统，虽然达到了良好的除冰效果，但电能消耗巨大。不论是从环保的角度还是适应新型飞机的变革，都需要对现有的除冰系统进行结构上的优化，或者是探索能耗更低，除冰效果更佳的除冰方案。电脉冲除冰系统，结构简单，能耗低，除冰效果优秀，是新型除冰系统的研究重点。国内不少专家与学者已展开了大量的研究工作。冰层的破坏规律，电脉冲除冰系统的除冰机理是研究的关键点之一。然而传统的有限元方法在模拟冰的破坏这类非连续问题时，很难克服网格依赖性，这种局限性的本源来自传统的连续介质理论的局部性。

近场动力学方法是由silling提出的一种来处理不连续问题的无网格方法，作为一种非局部理论，它采用位移函数积分形式的控制方程替代了经典固体力学中的偏微分方程，避免了基于连续性假设建模和求解空间微分方程的传统宏观方法在面临不连续问题时的奇异性，又突破了经典分子动力学方法在计算尺度上的局限，在宏/微观不连续力学问题分析中均表现出很高的求解精度和效率，因此在处理裂纹、损伤问题方面具有独特的优势。

发明内容

要解决的技术问题

为了避免基于传统有限元分析方法对除冰问题的局限性，比如难以克服网格依赖性，无法模拟裂纹的萌生和直观地反映冰层的裂纹扩展与剥离，本发明提出一种基于近场动力学理论的飞机电脉冲除冰模拟方法。

技术方案

本发明采用近场动力学方法对电脉冲除冰过程进行仿真模拟，利用这种新兴的基于连续介质非局部理论的无网格方法在不连续问题分析中的优势，构建电脉冲除冰系统的力学分析模型，对冰层的近场动力学材料参数、冰层在脉冲作用下力学响应特性与损伤规律、电脉冲除冰系统的性能等展开研究。

一种基于近场动力学理论的飞机电脉冲除冰模拟方法，其特征在于步骤如下：

步骤1：建立电脉冲除冰近场动力学仿真模型，所述的仿真模型包括蒙皮和附在蒙皮上的冰层；所述的仿真模型涉及的参数包括蒙皮的尺寸、杨氏模量、泊松比和密度；冰层的厚度、杨氏模量、泊松比和密度；所述的蒙皮的尺寸：长为A，宽为B，厚为H1；所述的冰层的厚度为H2；

步骤2：对仿真模型进行离散化、施加边界条件

将蒙皮和冰层均匀离散成体积一样的晶格，即物质点；根据物质点间距d确定模型中物质点的数量：再根据邻域半径δ构建所有物质点的邻域矩阵；

对机翼蒙皮施加边界条件：将蒙皮的相邻两边夹紧，进行固支；

电脉冲激励通过作用在圆形表面区域内的激振力载荷模拟；圆形表面与蒙皮表面不接触间距为0.1-0.5mm；电脉冲荷载瞬态分布规律遵循周期为T的正弦函数，荷载集度与距离的关系为：

其中：F(xi,t)为载荷集度，t为电脉冲荷载作用时长，R(xi)为物质点到载荷中心的距离与载荷半径的比值；

电脉冲荷载被转换为体积力均匀施加在靠近线圈的一层物质点上：

其中：为体积力，dx为物质点距载荷中心距离；

步骤3：构造冰-铝键函数和冰层剥离函数

基于双材料界面模型，建立冰铝界面键的键常数表达式：

其中：c为界面串联键的键常数，cA为冰的键常数，cB为铝的键常数，lA为冰键的原长，lB为铝键的原长，l为串联键的原长，ωA＝lB/l,ωB＝lA/l分别是冰和铝的距离加权函数；

将剪切破坏的断裂能Gs与通过界面的所有界面剪切键的能量进行等效，通过单位界面面积的所有界面剪切键达到临界伸长率的能量积分为：

根据剪切破坏的断裂能Gs的公式反推得到界面剪切键的临界伸长率Ss：

其中：c为冰-铝键的键常数，υc(j)为体积修正数；

将拉伸破坏的断裂能Gt与通过界面的所有键能之和进行等效，通过单位界面面积的所有界面拉伸键达到临界伸长率的能量积分为：

根据拉伸破坏的断裂能Gt的公式反推得到界面拉伸键的临界伸长率St：

将界面剪切键的临界伸长率SS和界面拉伸键的临界伸长率St，用于表征冰层与铝板间的剥离；

步骤4：迭代求解

将脉冲力转化为体积力进行施加，基于PD动力学方程，对仿真模型进行迭代，求解每一时间步物质点的位置和位移：

其中，ρ表示材料密度，u和分别表示物质点x的位移和加速度，Hx表示物质点x的近场范围，b表示体积力密度，t表示当前时刻，x′和u′分别表示物质点x近场范围Hx内任一点的物质点及其位移，dVx表示物质点x处的体积微元，f表示物质点x′作用在物质点x上矢量力；

根据位置和位移计算物质点间的伸长率s：

其中，η＝u(u′,t)-u(x,t)表示物质点的相对位移，ξ＝x′-x为物质点的相对位置；

对物质点间的伸长率s进行判断，若超过任一个临界伸长率，则对应方向的键断裂，键力消失；μ表示连接键的断裂状态：

其中，s0表示连接键的临界伸长率，当伸长率超过s0时，连接键破坏，两物质点间不再相互作用；

计算界面键的键力函数：

以连接键的破坏情况占比来表示各物质点邻域矩阵内局部破坏水平：

当冰层物质点邻域内所有的界面拉伸键和界面剪切键全部断裂时，即时，冰物质点完全从蒙皮表面剥离；因此，因此，电脉冲除冰系统的除冰率可由的冰层物质点在界面上的积分表示。

本发明进一步的技术方案：所述的蒙皮的材料为铝。

本发明进一步的技术方案：所述的蒙皮的杨氏模量为71.5GPa、泊松比为0.33、密度为2780kg/m3。

本发明进一步的技术方案：所述的冰层的杨氏模量为5.5GPa、泊松比为0.3、密度为897kg/m3。

本发明进一步的技术方案：所述的邻域半径δ为3.015mm。

本发明进一步的技术方案：所述的圆形表面区域直径为60mm。

有益效果

本发明方法基于键基近场动力学理论建立了电脉冲除冰系统的数值模型，模拟高应变率状态下冰层与蒙皮的动力学响应，构建了相邻两边固支的电脉冲除冰系统平板模型，通过对除冰过程的动态模拟与现有的有限元模型进行对比，验证了近场动力学模型的正确性。讨论了冰层的损伤、表面裂纹扩展、冰层剥离率随时间的变化规律，研究了电脉冲作用半径D、强度F对蒙皮损伤以及除冰率的影响，对电脉冲除冰系统线圈圈数以及安装位置有指导意义。

附图说明

附图仅用于示出具体实施例的目的，而并不认为是对本发明的限制，在整个附图中，相同的参考符号表示相同的部件。

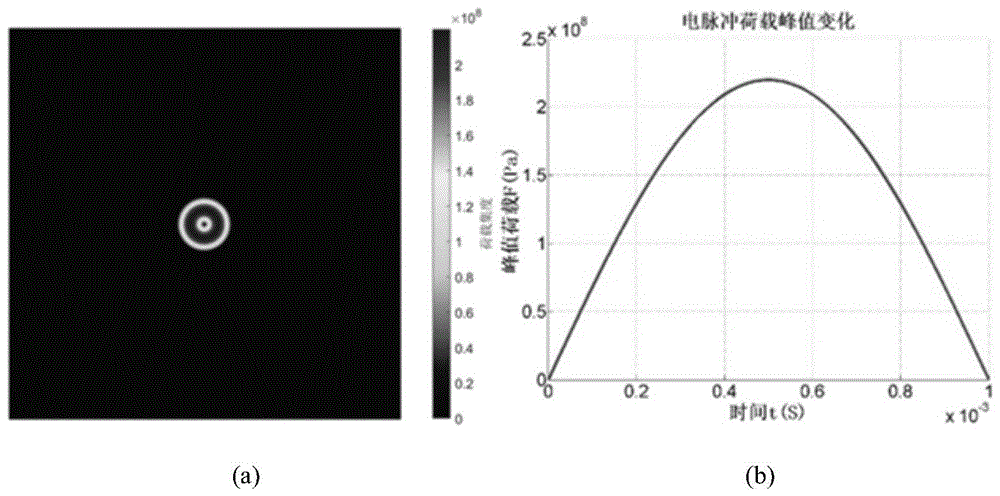
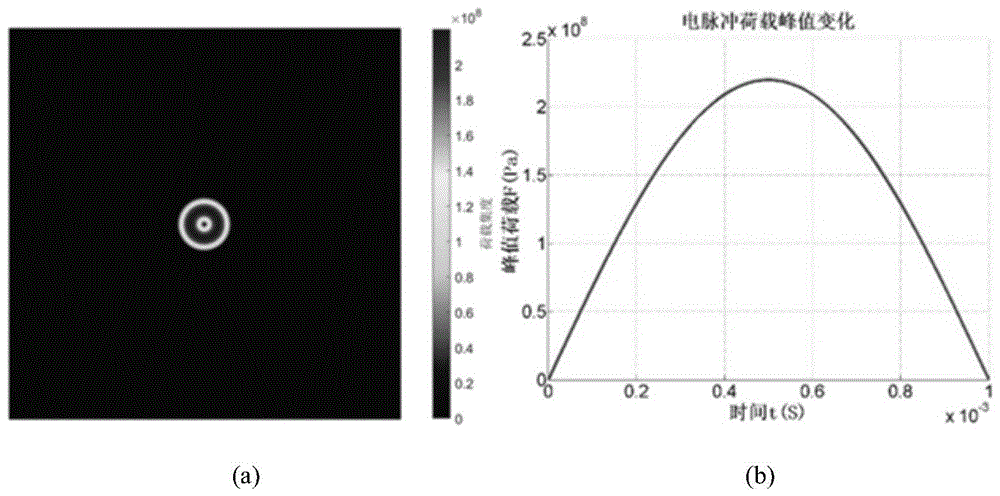
图1为电脉冲荷载分布规律及峰值变化规律示意图：(a)电脉冲荷载分布规律；(b)荷载峰值变化规律；

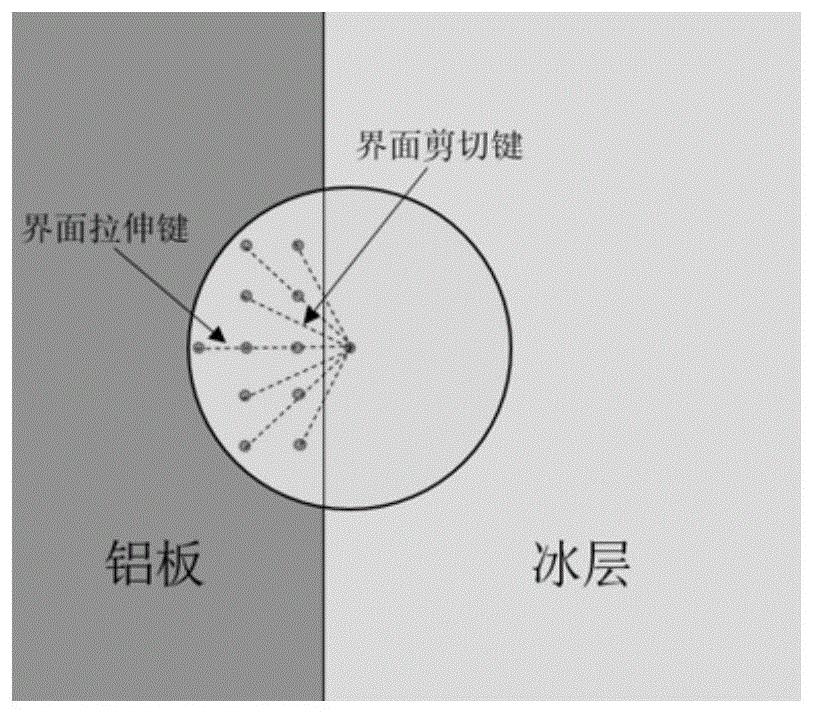
图2为冰铝界面混合键模型示意图；

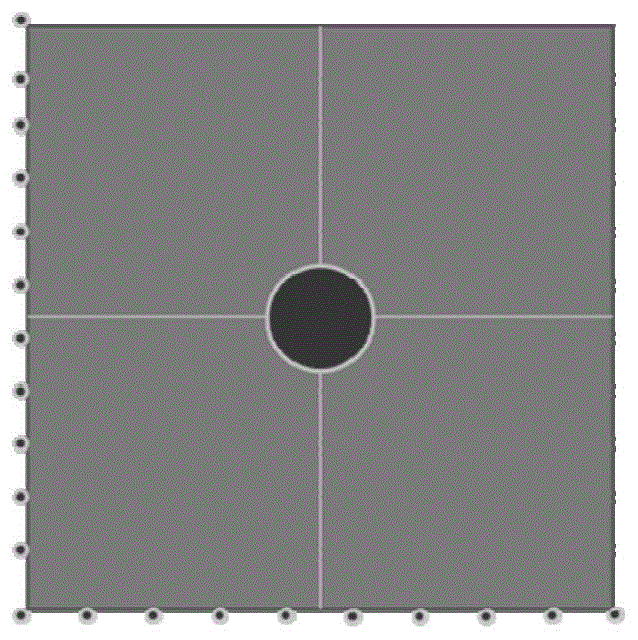
图3为电脉冲除冰系统模型示意图；

图4为双边固支模型冰层裂纹扩展的示意图；

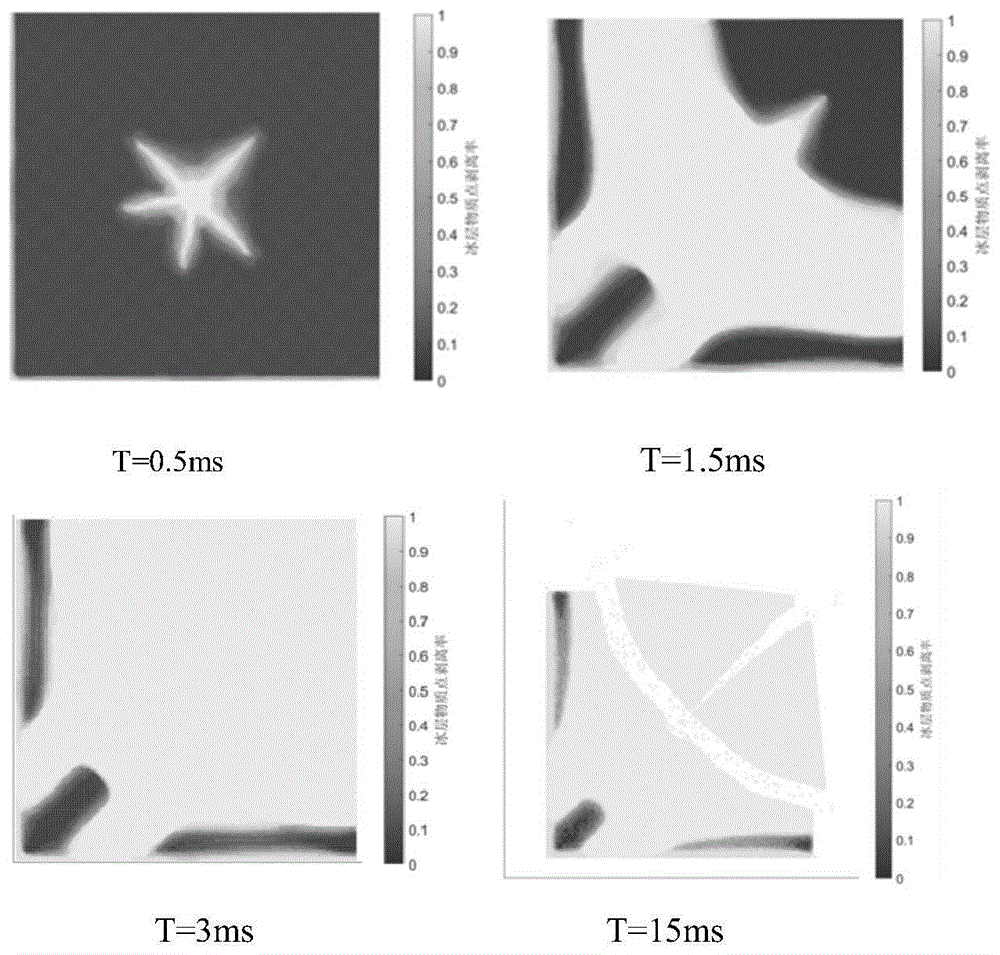
图5为双边固支模型冰层剥离的示意图；

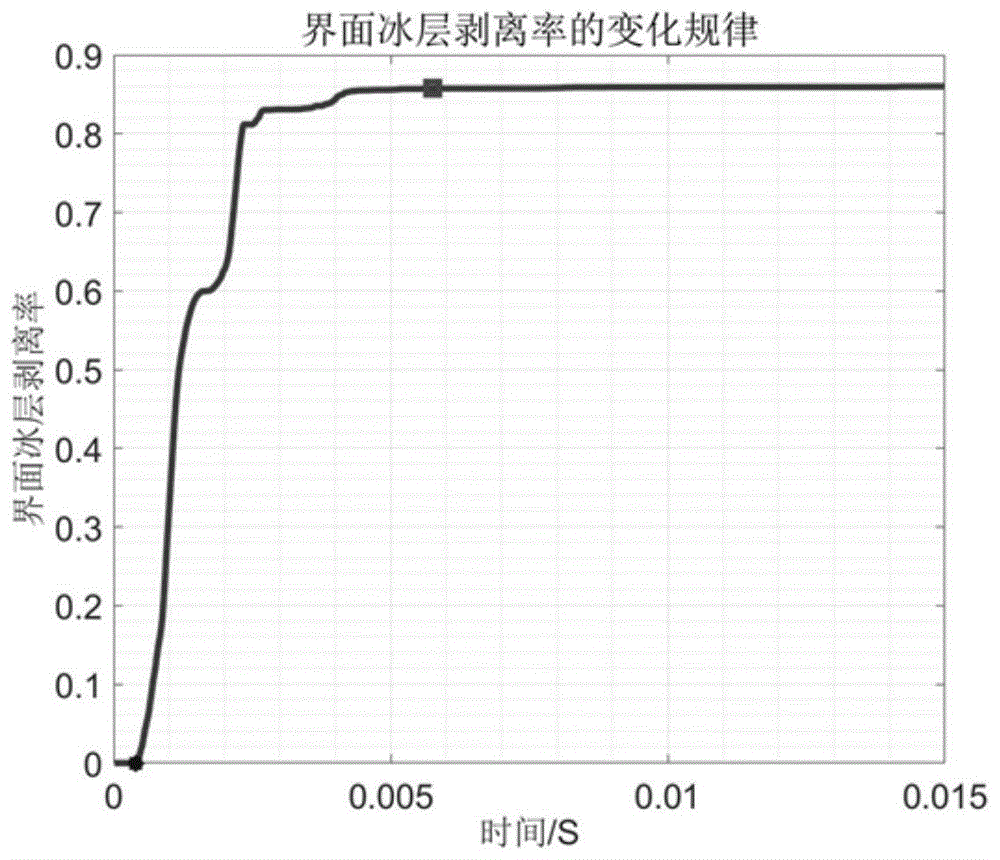
图6为冰层剥离率随时间的变化示意图；

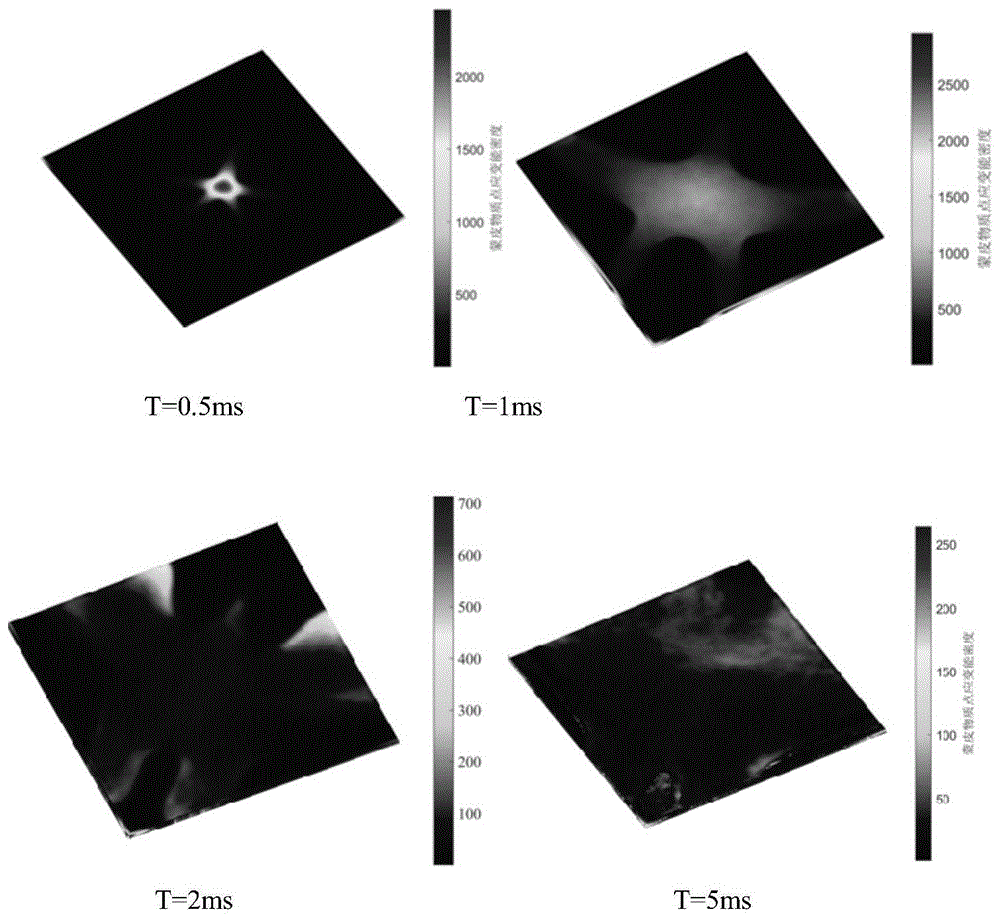
图7为机翼蒙皮应变能分布云图；

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图和实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。此外，下面描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

本发明以铝制机翼蒙皮为例，对其进行如下一系列的模拟分析：

第一步：建立电脉冲除冰的仿真模型，仿真模型为方形铝制蒙皮，铝制蒙皮长为A＝420mm，宽为B＝420mm，厚为H1＝2mm，表面上附有厚度为H2＝3mm的冰层。蒙皮的杨氏模量为71.5GPa，泊松比为0.33，密度为2780kg/m3，冰层的杨氏模量为5.5GPa，泊松比为0.3，密度为897kg/m3。

在近场动力学理论当中，将外荷载转换为体积力施加在真实材料点上。由于电磁感应的趋肤效应，电流会集中在靠近线圈区域，沿着蒙皮法向向外电流越小。因此，当蒙皮厚度小于趋肤厚度时，蒙皮厚度也大，电磁力越大，沿蒙皮厚度方向上均存在电磁力。反之，若蒙皮较厚，随着蒙皮增厚，电磁力趋于平稳。

电脉冲除冰系统在蒙皮上产生的电脉冲激振力是由电磁感应现象引起的排斥力，电脉冲激振力瞬态分布规律遵循周期为T的正弦函数，表达式为：

其中：F(xi,t)为载荷集度，t为电脉冲荷载作用时长，R(xi)为物质点到载荷中心的距离与载荷半径的比值。

电脉冲荷载集度与距离的关系如图1所示，电脉冲荷载中心区域，荷载大小不变，荷载分布呈中心对称，大小随坐标距中心距离呈线性递减，直至距离荷载中心1.5倍线圈半径处时荷载大小为零。在建模中，将脉冲载荷转化为体积力施加在铝制蒙皮表面。

将电脉冲荷载转换为体积力均匀施加在靠近线圈的一层物质点上：

其中：为体积力，F为电脉冲荷载，dx为物质点距载荷中心距离。

第二步：对仿真模型进行离散，根据物质点间距d＝1mm确定了物质点的数量N＝882000，选取近场范围为3.015倍的物质点半径，即δ＝3.015mm，构建所有物质点的邻域矩阵，时间步长为150000步，总时间为15ms。将铝制蒙皮的相邻两边夹紧，进行固支，如图3所示，电脉冲激励通过作用在圆形表面(直径为60mm)上的激振力载荷模拟。

第三步：构造冰-铝键力函数

在距离加权键串联界面模型中，冰-冰键A和铝-铝键B内力相等：

f＝cs＝cAsA＝cBsB

sA＝ΔlA/lA

sB＝ΔlB/lB

s＝(ΔlA+ΔlB)/l

其中f为键力函数，c为界面串联键的键常数，cA为冰的键常数，cB为铝的键常数，ΔlA为冰键的伸长量，ΔlB为铝键的伸长量，lA为冰键的原长，lB为铝键的原长，l为串联键的原长。sA为冰键的伸长率，sB为铝键的伸长率，s为串联键的伸长率。

联立上述公式可解得界面键的键常数表达式：

上式对字母A、B具有轮换对称性，故引入距离加权函数对表达式进行简化：

令ωA＝lB/l,ωB＝lA/l

第四步：确定临界伸长率

根据键的初始构型将冰-铝混合键分为两类，如图2所示，现定义与界面垂直的键为界面拉伸键，与界面不垂直的为界面剪切键。两种键的键常数相同，均由串联混合键模型确定。

冰-铝界面上的剪切破坏视为划开型裂纹，将剪切破坏的断裂能Gs与通过界面的所有界面剪切键的能量进行等效，通过单位界面面积的所有界面剪切键达到临界伸长率的能量积分为：

Wpds＝Gs

根据剪切破坏的断裂能Gs的公式反推得到界面剪切键的临界伸长率Ss：

其中：c为冰-铝键的键常数，υc(j)为体积修正数；

冰-铝界面上的拉伸破坏视为张开型裂纹，拉伸变形会引起包括界面剪切键在内的所有穿过冰-铝界面的键能变化。因此将拉伸破坏的断裂能Gt与通过界面的所有键能之和进行等效，通过单位界面面积的所有界面拉伸键达到临界伸长率的能量积分为：

Wpdt+Wpds＝Gt

根据拉伸破坏的断裂能Gt的公式反推得到界面拉伸键的临界伸长率St：

第五步：将脉冲力转化为体积力进行施加，基于PD动力学方程，对仿真模型进行迭代，求解每一时间步物质点的位置和位移：

其中，ρ表示材料密度，u和分别表示物质点x的位移和加速度，Hx表示物质点x的近场范围，b表示体积力密度，t表示当前时刻，x′和u′分别表示物质点x近场范围Hx内任一点的物质点及其位移，dVx表示物质点x处的体积微元，f表示物质点x′作用在物质点x上矢量力；

根据位置和位移计算物质点间的伸长率s：

其中，η＝u(u′,t)-u(x,t)表示物质点的相对位移，ξ＝x′-x为物质点的相对位置；

对物质点间的伸长率s进行判断，若超过任一个临界伸长率，则对应方向的键断裂，键力消失；μ表示连接键的断裂状态，

其中，s0表示连接键的临界伸长率，当伸长率超过s0时，连接键破坏，两物质点间不再相互作用；

计算界面键的键力函数：

以连接键的破坏情况占比来表示各物质点邻域矩阵内局部破坏水平：

当冰层物质点邻域内所有的界面拉伸键和界面剪切键全部断裂时，即时，冰物质点完全从蒙皮表面剥离；因此，电脉冲除冰系统的除冰率可由剥离率为1的冰层物质点在界面上的积分表示。

从冰层的剥离和损伤图中可以看出本发明建立的近场动力学模型与有限元分析吻合良好。同时，近场动力学模型展现出来冰层裂纹的萌生，直观地展现了裂纹的扩展路径和破坏形式。

双面固支平板电脉冲除冰模型的动态响应如图4所示，在5ms以后冰层的损伤与剥离趋于稳定，最终仅在固定端附近区域，有少量的冰残留，除冰效果非常显著。在电脉冲荷载作用下，脉冲中心区域蒙皮发生显著变形，因此冰层在电脉冲荷载中心区域出现初始裂纹，随后形成五条主裂纹分别向四条边界扩展，其中有一条沿着平板对角线向自由边界延伸。向自由边界延伸的裂纹最终导致部分冰层的碎裂与剥离。随着靠近自由边界部分结构的形变增大，当T＝1.55ms时自由边界未剥离区域萌生出新的裂纹，最终两条裂纹汇集贯穿，被贯穿裂纹包围的冰层随之剥离。

冰层与蒙皮间的剥离瞬态分析如图5所示，由于模型中冰层厚度仅为3mm，冰层从蒙皮表面剥离的演化规律与冰层表面的裂纹扩展形式相符。

电脉冲除冰系统冰层剥离率随时间的变化如图6所示，界面冰层在0.39ms开始从蒙皮上剥离，电脉冲荷载作用时间为1ms，在此期间冰层剥离率急剧上升，从图中数据可以看出，在电脉冲激励消失后，冰层随蒙皮做自由振动，冰层的剥离率阶段性增大。在5.75ms，冰层的剥离率(除冰率)达到85.76％，随后数值趋于稳定，最终冰层的剥离率为86.04％。

通过应变能密度，可以直观反映应力的集度。在整个除冰过程中，机翼蒙皮中应变能密度的分布规律如图7所示。随着电脉冲荷载的施加，荷载作用中心和冰层裂纹附近蒙皮的应变能密度较高，在1ms后，电脉冲荷载消失，蒙皮应变能随着冰层的损伤与剥离逐渐耗散。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明公开的技术范围内，可轻易想到各种等效的修改或替换，这些修改或替换都应涵盖在本发明的保护范围之内。