技术领域

本发明属于光伏电池领域，涉及光伏电池参数的稳健优化。建立光伏电池模型，基于给定的约束条件，对光伏电池参数进行稳健优化设计，采用蒙特卡洛法求解优化设计模型，实现对光伏电池的稳健优化设计。

背景技术

目前，世界能源供应绝大部分来自化石能源，人类正逐步面临环境污染和资源短缺的问题。为实现可持续发展目标，就需要发展和应用零污染的清洁可再生能源。在各种可再生能源中，太阳能被视为最有前途的能源，通过光伏效应，光伏电池可以直接将光能转化为电能，在能源领域前景广阔，具有重要的战略地位。

当前对光伏电池的研究大都是基于光照强度和工作温度的变化，讨论外部环境变化对光伏电池输出性能的影响。但在实际生产生活中，影响光伏电池性能的部件如二极管、电阻、电池板等，由于材料选取的不确定和制作工艺不同等因素的存在，都会给光伏电池的输出带来很大影响。这些不确定性都会给电网规划、系统调度和电网的可靠、稳定运行带来诸多问题。因此，对光伏电池进行优化设计，确定构件材料和制造工艺的选取，让光伏电池稳定可靠的运行已迫在眉睫。

在过去的几十年里，人们开发了各种不确定性传播的概率建模方法。其中，基于抽样的不确定度传播的蒙特卡罗方法是使用最普遍广泛的，该方法主要是通过对不确定性模型问题中的设计变量或设计参数进行随机抽样，然后利用随机样本来求解问题概率的一种统计学方法，具有普遍的适用性和典型的稳健性。在结构、系统或解决方案性能的最高量化水平上，基于蒙特卡罗的不确定性分析是一个常见的过程。本专利用蒙特卡洛法来求解稳健优化模型，实现对光伏电池的稳健优化设计。

发明内容

要解决的技术问题

传统的光伏电池优化目的都是使输出功率最大化，却忽略了输出的稳定性，没法保证电池的可靠运行。为了避免现有技术的不足之处，本发明提出一种光伏电池的稳健性优化设计方法。

技术方案

一种光伏电池的稳健性优化设计方法，其特征在于步骤如下：

步骤1：以光伏构件材料参数为设计变量x，实际工作环境中的温度和辐照强度为设计参数z，其具体分布情况如下表1所示：

表1光伏电池设计变量和设计参数的分布情况

将光伏电池的最大输出功率作为优化目标，将所研究电池的理论效率作为约束性能函数，建立确定性优化模型如下：

Find x1 x2 x3 x4

Max P(x,z)

s.t.g(x,z)＝η(x,z)-0.159≤0

0.286≤x1≤0.656，802.24≤x2≤1602.24

0.0059≤x3≤0.0061，1.18≤x4≤1.6

使用蒙特卡洛法求解确定性优化模型，得到优化目标最大输出功率值Pmax及其对应的设计变量值x＝{x1,x2,x3,x4}；

步骤2：将确定性优化得到的设计变量值作为稳健优化设计变量均值的初始点μx′＝{x1,x2,x3,x4}，转换得到基于均值和标准差的稳健优化模型，表示如下：

Find

Min

s.t.G(x,z)＝μg(x,z)≤0

步骤3：使用蒙特卡洛法求解稳健优化模型，得到设计变量均值根据求得的μx选取光伏构件对应的材料和制作工艺，实现光伏电池的稳健优化设计。

有益效果

本发明提出的一种光伏电池的稳健性优化设计方法，建立稳健优化模型，对优化模型求解，得到了对应设计变量的值。虽然确定性优化模型下光伏电池的输出功率比稳健优化模型下的输出功率略大，但稳健优化后约束条件的标准差和失效概率都比确定性优化的小，输出波动变小，提高了光伏电池输出的稳定性和可靠性，对光伏电池输出性能的研究具有重要意义，提升了光伏电池的应用水平。

附图说明

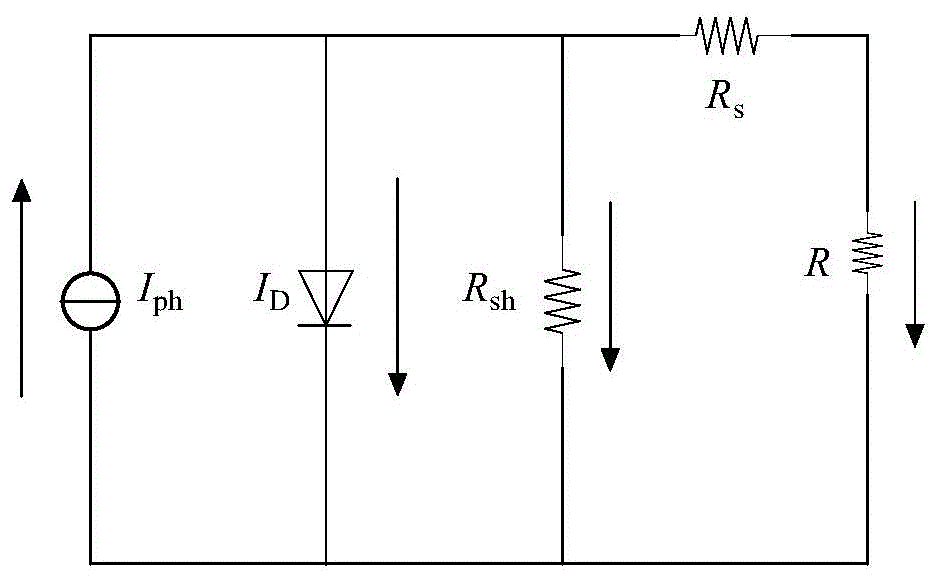
图1光伏电池的等效电路图

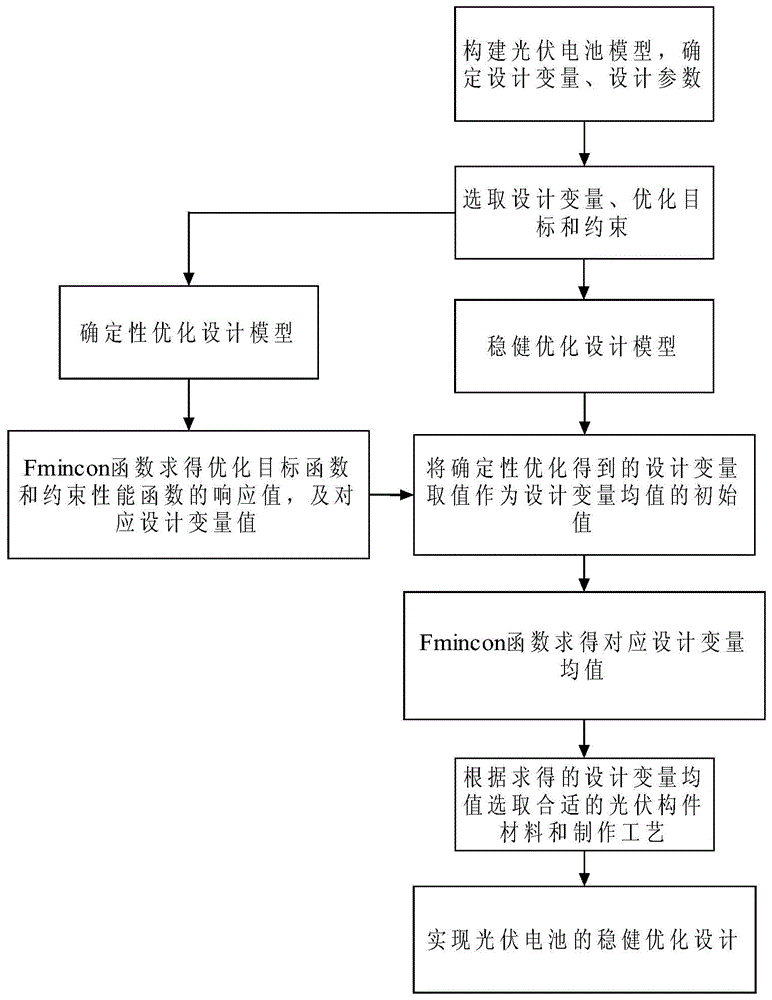
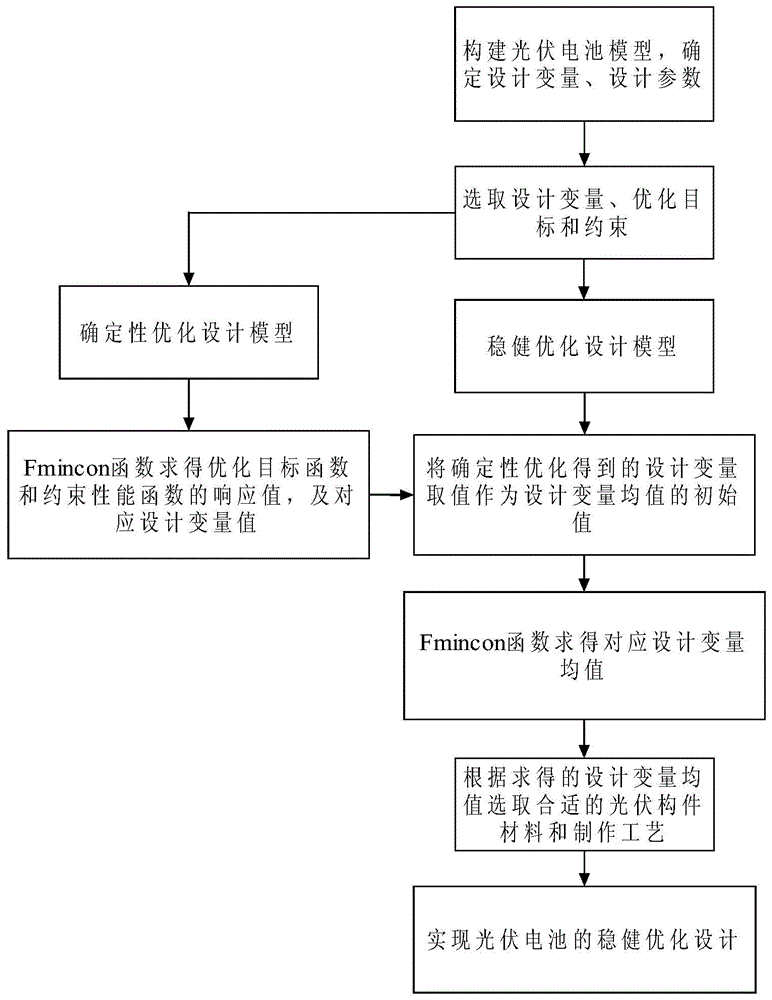
图2光伏电池稳健优化设计流程图

具体实施方式

现结合实施例、附图对本发明作进一步描述：

本发明以光伏电池输出的可靠性和稳定性为目标，考虑光伏电池实际工作环境的随机性和光伏构件材料属性的区间不确定性，将受随机与区间不确定性共同影响的光伏电池输出功率的标准差与均值的最小比值作为优化目标，将给定的理论转换效率作为约束性能函数，建立稳健优化模型，并采用蒙特卡洛法求解。流程图如图2所示，包括以下步骤：

步骤1：建立光伏电池模型

光伏电池等效电路是由产生光生电流的恒流源和一系列电阻(内部并联电阻Rsh和串联电阻Rs)构成，如图1所示。

由光伏电池的等效电路可得：

I＝Iph-ID-Ish (1)

由二极管的原理可得：

根据基尔霍夫原理可得：

联立公式(1)，(2)，(3)可得：

公式(1)(2)(3)和(4)中：I为光伏电池输出电流；Iph为光生电流；ID为二极管的电流；Ish为流过光伏电池等效并联电阻的电流；Io为二极管反向饱和电流；V为光伏电池输出电压；q为电子电荷；n为二极管影响因子；K为玻尔兹曼常数；T为光伏电池表面温度；Rs为光伏电池等效串联电阻；Rsh为光伏电池等效并联电阻。

为了方便后续计算，需得出电流显式方程，使方程右边不含电流项。由Lambert W函数给出电流显式方程为：

其中，

在公式(4)中，Iph和Io这两个模型参数，均为温度和光强的函数。其计算式为：

公式(7)和(8)中，S为辐照强度；T为电池温度；C短路电流温度系数；Eg为材料禁带宽度，其温度特性为Eg/Eg,ref＝1-1.0002677(T-Tref)；下标ref表示在标准测试条件下。

则可求得输出功率P如下式所示：

光伏电池的转换效率η为

式中，Vm为最大功率点电压；Im为最大功率点电流；A为电池面积。

光伏电池的输出性能受实际工作环境的影响，同时光伏电池中的二极管、电阻和电池板这些光伏构件，由于制造、安装误差以及材料的分散性等不可避免的因素会导致构件参数不确定性，在随机工作环境和参数不确定性共同作用下，光伏电池的输出会产生很大变化。以光伏构件材料参数为设计变量x，实际工作环境中的温度和辐照强度为设计参数z，其具体分布情况如下表1所示。

表1光伏电池设计变量和设计参数的分布情况

步骤2：建立稳健优化设计模型

将光伏电池的最大输出功率作为优化目标，将所研究电池的理论效率作为约束性能函数，建立确定性优化模型如下：

Find x1 x2 x3 x4

Max P(x,z)

s.t.g(x,z)＝η(x,z)-0.159≤0

0.286≤x1≤0.656，802.24≤x2≤1602.24

0.0059≤x3≤0.0061，1.18≤x4≤1.6

考虑到设计变量的均值更加能反映真实的结果，以原始设计变量的均值作为新模型中的设计变量，由上述的确定性优化设计模型可以转换得到基于均值和标准差的稳健优化模型，表示如下：

Find

Min

s.t.G(x,z)＝μg(x,z)≤0

步骤3：对稳健优化模型进行求解

蒙特卡洛法是一种基于随机抽样来求解数值解不确定情况下的一种有效的近似模拟方法。该方法主要是通过对不确定性模型问题中的设计变量或设计参数进行随机抽样，然后利用随机样本来求解问题概率的一种统计学方法。蒙特卡洛法是一种非常直接简单的估计计算法，它求解均值和方差的表达式如下：

其中，N是样本数，xi和zi分别是设计变量和设计参数的样本点。

蒙特卡洛法求解约束条件的失效概率的积分式如下式(12)所示。

其中f(X)为变量X＝{x1,x2,x3,x4,z1,z2}的联合概率密度函数，F为不满足约束条件的失效域，Pf是失效概率。

求解具体过程如下：

先运用蒙特卡洛法求解确定性优化模型，得到优化目标最大输出功率值及其对应的设计变量值x＝{x1,x2,x3,x4}如表2行2所示，再将确定性优化得到的设计变量值作为稳健优化设计变量均值的初始点μx′＝{x1,x2,x3,x4}，再用蒙特卡洛法求解稳健优化模型，得到设计变量均值μx＝{μx1,μx2,μx3,μx4}如表2行3所示，根据求得的μx选取光伏构件对应合适的材料和制作工艺，实现光伏电池的稳健优化设计。

实施例1：

第一步：建立光伏电池模型，并由工程经验确定光伏电池的设计变量x1,x2,x3,x4和设计参数z1,z2，并给定设计变量x的取值范围，具体分布情况如表1所示。

第二步：将光伏电池的最大输出功率作为优化目标，理论效率作为约束性能函数，建立传统确定性优化模型；再以原始设计变量的均值作为新模型中的设计变量，把光伏电池输出功率标准差和均值的最小比值作为优化目标，理论效率的均值作为约束性能函数，将确定性优化设计模型转换为基于均值和标准差的稳健优化模型。

第三步：采用简单随机抽样完成对设计变量和设计参数的初始采样，以设计变量x为独立控制参数，利用matlab中的Fmincon函数，得到确定性优化目标函数和约束性能函数的响应值，及对应的设计变量取值{0.286,1602.24,0.0061,1.6}；将确定性优化得到的设计变量x＝{0.286,1602.24,0.0061,1.6}作为稳健优化设计变量均值的初始点，同样利用matlab中的Fmincon函数，得到稳健优化目标函数和约束性能函数的响应值，及对应的设计变量均值取值μx＝{0.4778,1601.2452,0.005996,1.3874}，根据求得的μx选取对应光伏构件合适的材料和制作工艺，实现光伏电池的稳健优化设计。

x和μx均服从正态分布。由式(10)和(11)可以分别求得确定性优化和稳健优化约束条件的均值和方差，如表3所示。再由式(12)可以分别求得确定性优化和稳健优化约束条件失效时的失效概率，如表4所示。(为了方便计算，N取100000)。虽然确定性优化模型下光伏电池的输出功率比稳健优化模型下的输出功率略大，但稳健优化后约束条件的标准差和失效概率都比确定性优化的小，输出波动变小，提高了光伏电池输出的稳定性和可靠性。

表2优化模型计算结果

表3稳健优化与确定性优化结果

表4不同优化结果下约束条件的失效概率