技术领域

本发明属于可靠性领域，涉及复合材料加筋壁板后屈曲的可靠性分析，具体涉及一种基于自适应重要抽样的复合材料加筋壁板后屈曲可靠性分析方法。

背景技术

复合材料由于具有比强度高、比刚度高和可设计性强等优点，在航空领域得到了广泛应用。复合材料在航空结构中常以层合板、层合壳的形式出现，这些结构一般较薄，常通过设置加强筋来增强整体刚度或局部刚度。加筋结构的主要破坏模式是结构丧失稳定性。为了保证和提高复合材料加筋壁板的设计性和使用安全性，对结构进行极限承载能力的可靠性分析就显得尤为重要。

可靠性是度量产品质量的重要指标。可靠度是衡量产品或系统价值的一个重要标准,拥有高度的可靠性会为产品或系统的提供者带来极大的竞争优势,可靠性理论和方法已被广泛应用于航空领域。人们在复合材料结构的可靠性评估方面进行了大量的工作。

当前复合材料结构的可靠性评估常用的分析方法有近似解析法和蒙特卡洛法等。近似解析法仅适用于具有特殊几何边界和加载条件的问题,难以解决具有复杂边界和加载条件的问题；蒙特卡洛法以均值点处为抽样中心，计算精度高,但抽样效率低，收敛较慢，计算代价大,通常作为检验其他方法的工具。为此，需要高效的抽样方法，来解决复合材料加筋壁板后屈曲的可靠性问题。

自适应重要抽样通过在计算过程中不断自适应修正抽样函数中心，尽可能多的在对结果影响重大的“重要区域”进行抽样，减少对模拟结果无关紧要的事件的抽样，以达到提过计算效率的目的。相对于蒙特卡洛法，自适应抽样法具有更高的精度，且得到收敛解的模拟次数小于蒙特卡洛法的模拟次数，提高了模拟计算的效率。

发明内容

要解决的技术问题

为了避免现有技术的不足之处，本发明提出一种基于自适应重要抽样的复合材料加筋壁板后屈曲可靠性分析方法。

技术方案

一种基于自适应重要抽样的复合材料加筋壁板后屈曲可靠性分析方法，其特征在于步骤如下：

步骤1：给定复合材料加筋壁板相关变量X＝{X1,X2,…,X8}的均值和标准差，参数X1～X8均服从正态分布；其中X1为复合材料板的厚度、X2为铺层的角度、X3为蒙皮宽度、X4和X5为水平缘条的宽度、X6为缘条高度、X7为加筋层合板的长度，X8为加筋壁板所受的实际载荷；复合材料加筋壁板参数的概率特性如下表所示：

参数 标识 均值 标准差 分布类型 厚度/mm X1 0.125 0.00125 正态 铺层角度/° X2 0 0.1 正态 蒙皮的宽度/mm X3 710 0.071 正态 水平缘条1的宽度/mm X4 55 0.0055 正态 水平缘条2的宽度/mm X5 25 0.0025 正态 缘条的高度/mm X6 45 0.0045 正态 加筋层合板的长度/mm X7 570 0.057 正态 实际载荷/N X8 1.256×106 1×104 正态

步骤2：对步骤1的参数进行正态抽样，利用自适应抽样法计算失效概率：

(1)第1次抽样，即q＝1，选择第1次重要抽样函数为h(1)(X)为正态型，h(1)(X)的抽样中心ΔX(1)为均值点，方差向量与输入向量的联合概率密度函数的方差向量一致，即μh(1)＝μX＝{0.125,0,710,55,25,45,570,1.256×106}T，方差向量按照重要抽样函数h(1)(X)抽取N(1)个样本X(1)s(s＝1,2,…,N(1))，判断样本X(1)s(s＝1,2,…,N(1))是否落入失效域Rn；对于落入Rn区域的抽样点，采用下式计算失效概率并将当前联合概率密度函数f(X)最大值对应的样本点记为δ*；第2次重要抽样函数为h(2)(X)的抽样中心ΔX(2)即为δ*，方差向量与输入向量的联合概率密度函数的方差向量一致；

其中，下标q表示抽样次数，q＝1,2,…,m，IF(X(q)s)为指示函数，f(X(q)s)为当前联合概率密度函数，h(q)(X(q)s)为重要抽样函数；

(2)第q次的重要抽样密度函数h(q)(X)为正态型，抽样中心为ΔX(q)，方差向量与输入向量的联合概率密度函数的方差向量一致，即μh(q)＝Δx(q)，方差向量按照重要抽样函数h(q)(X)抽取N(q)个样本X(q)s(s＝1,2,…,N(q))，判断样本X(q)s(s＝1,2,…,N(q))是否落入失效域Rn；对于落入Rn区域的抽样点，采用式(7)计算失效概率并将当前f(X)最大值对应的样本点记为δ*；比较ΔX(q)和δ*对应的联合概率密度函数f(ΔX(q))和f(δ*)的大小；如果f(δ*)≥f(ΔX(q))，则第q+1次的重要抽样密度函数h(q+1)(X)的抽样中心ΔX(q+1)选为δ*；如果f(δ*)＜f(ΔX(q))，则第q+1次的重要抽样密度函数h(q+1)(X)的抽样中心ΔX(q+1)选为ΔX(q)；

(3)进行m次抽样，采用下式计算加筋壁板结构的失效概率

所述的步骤2中m取20，N(q)均取100000。

有益效果

本发明提出的一种基于自适应重要抽样的复合材料加筋壁板后屈曲可靠性分析方法，运用半经验公式计算加筋壁板后屈曲的极限载荷，对加筋壁板结构不确定性变量进行研究，采用自适应重要抽样法对复合材料加筋壁板后屈曲进行可靠性分析，高效快速的得到后屈曲的失效概率，实现复合材料加筋壁板结构的可靠性评估。

本发明通过自适应重要抽样方法研究了复合材料加筋壁板后屈曲的可靠性，计算了其失效概率。运用自适应抽样法求得的失效概率更快趋于稳定，得到收敛解的模拟次数大大小于蒙特卡洛法的模拟次数，提高了模拟计算的效率。本方法能高效快速地对复合材料加筋壁板后屈曲进行可靠性分析，对复合材料加筋壁板后屈曲的研究有重要意义，提升了复合材料的应用水平。

附图说明

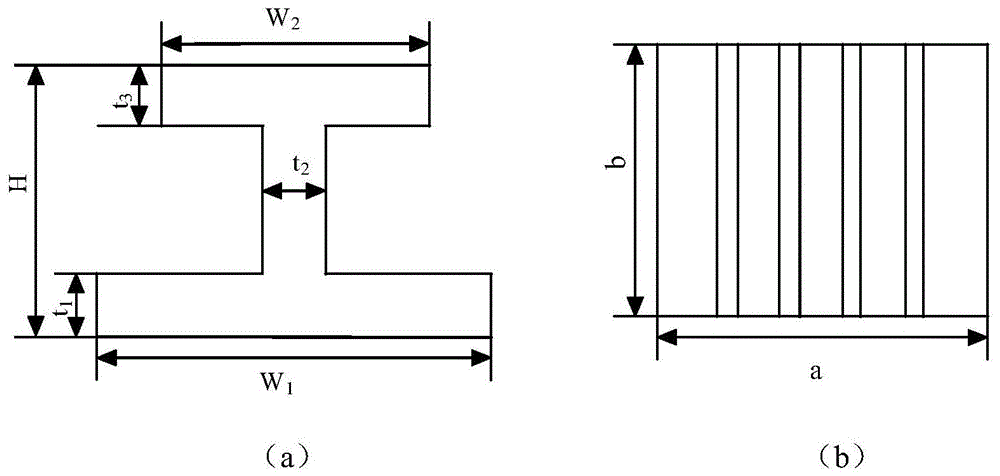
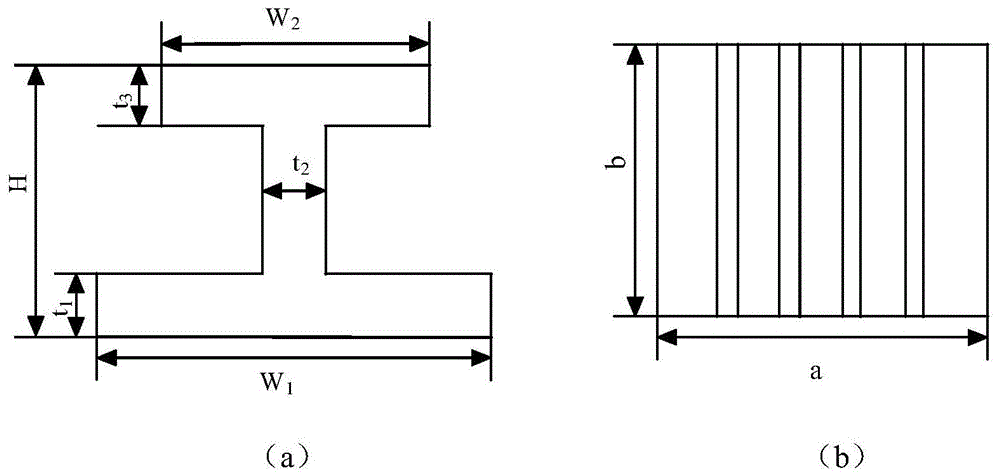
图1复合材料加筋壁板结构简图

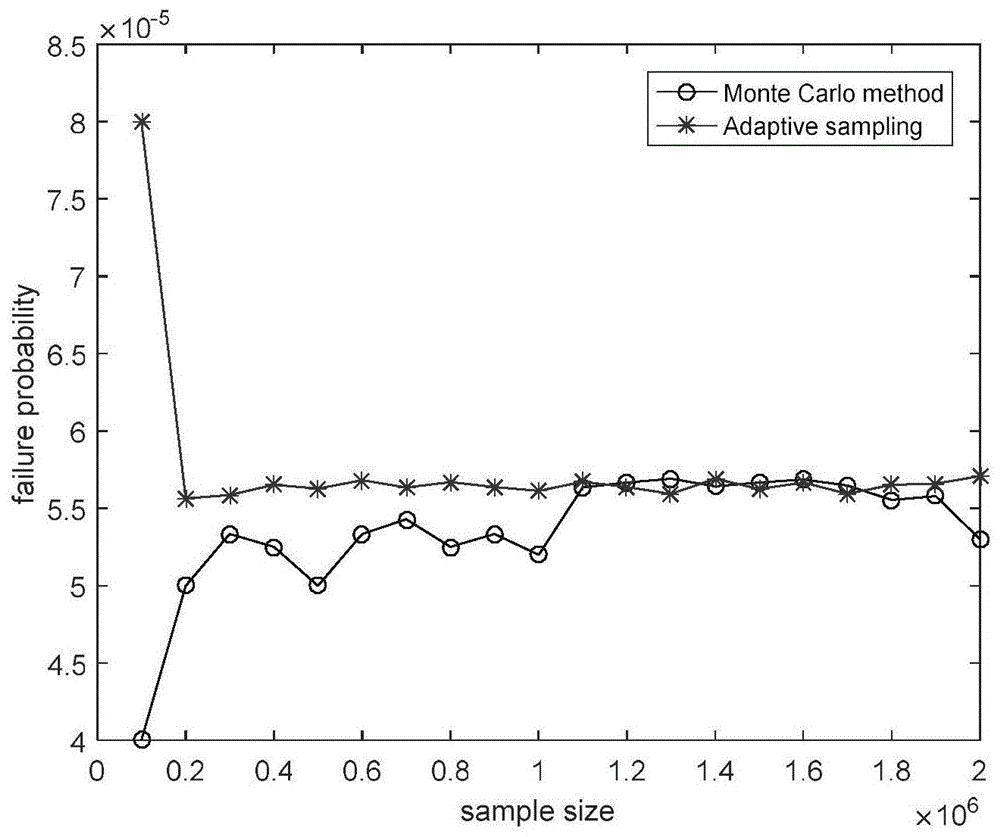
图2失效概率图

具体实施方式

现结合实施例、附图对本发明作进一步描述：

复合材料加筋壁板结构后屈曲失效建模

图1所示为加筋壁板的结构简图，由于加筋壁板结构材料性能的分散性，以及制作工艺上的误差，会有结构尺寸的偏差，结合工程经验以及理论上的分析，复合材料板的厚度X1、铺层的角度X2、蒙皮宽度X3、水平缘条的宽度X4和X5缘条高度X6及加筋层合板的长度X7为极限载荷的隐函数。

可以通过ANSYS分析及由《复合材料结构稳定性分析指南》一书中所给的半经验公式得到加筋壁板的破坏载荷Load{X1,X2,…,X7}。

加筋壁板后屈曲的极限状态方程为g(X)＝Load{X1,X2,…,X7}-X8 (1)

式中：变量X＝{X1,X2,…,X8}，X8为加筋壁板所受的实际载荷。

当g(X)＜0时，加筋壁板后屈曲失效，X落入失效域Rn；当g(X)≥0时，未失效，X落入安全域Rs。

影响复合材料加筋壁板后屈曲可靠性的参数如下表1所示。

表1复合材料加筋壁板参数的概率特性

参数 标识 均值 标准差 分布类型 厚度/mm X1 0.125 0.00125 正态 铺层角度/° X2 0 0.1 正态 蒙皮的宽度/mm X3 710 0.071 正态 水平缘条1的宽度/mm X4 55 0.0055 正态 水平缘条2的宽度/mm X5 25 0.0025 正态 缘条的高度/mm X6 45 0.0045 正态 加筋层合板的长度/mm X7 570 0.057 正态 实际载荷/N X8 1.256×106 1×104 正态

基于自适应抽样法对加筋壁板后屈曲进行可靠性分析

复合材料加筋壁板后屈曲可靠性分析的传统方法为蒙特卡洛法，蒙特卡洛法求解失效概率的积分式如下式所示。

其中f(X)为变量X＝{X1,X2,…,X8}T的联合概率密度函数，Rn为失效域，Pf是失效概率，是复合材料加筋壁板后屈曲可靠性评价的重要指标。

根据变量的联合概率密度函数f(X)抽取输入向量变量X的N个样本{X1,X2,…,XN}T,则失效概率的估计值为如下式(3)所示。

其中，Xs是通过联合概率密度函数f(X)抽取的第s(s＝1,2,…,N)个样本，I(X)是指示函数，Nf是落在失效域的样本数，N是总的抽样数。

蒙特卡洛法需要抽取大量的样本才能得到收敛的结果，抽样效率很低。因此研究人员提出了改进的数字模拟法，重要抽样法是其中常见的一种。引入重要抽样密度函数h(X)，将求解失效概率的积分式转化为如下式(4)所示的形式。

根据重要抽样密度函数h(X)抽取输入变量X的N个样本，则失效概率的估计值如下式(5)所示。

采用重要抽样法求解复合材料加筋壁板后屈曲的可靠性问题的难点在于选择合适的重要抽样函数h(X)。针对简单的显式功能函数g(X)，可以通过改进一次二阶矩方法求解得到。对于复合材料加筋壁板后屈曲问题，其功能函数g(X)形式复杂，很难通过改进一次二阶矩方法直接求解得到。

因此，引入自适应重要抽样法来求解复合材料加筋壁板的后屈曲可靠性问题。对于自适应重要抽样函数hq(X)，抽取的样本数为N(q)。

式中：下标q表示抽样次数，q＝1,2,…,m。

则最终基于自适应重要抽样法的失效概率估算如下式(8)所示。

根据上述自适应重要抽样法的原理，计算复合材料加筋壁板后屈曲的可靠性的步骤如下。

第一步：根据实际工程情况，给定复合材料加筋壁板相关变量X1～X7的均值和标准差，实际载荷X8的均值和标准差，参数均服从正态分布，具体概率特性如表1所示；

第二步：将均值点作为第一次抽样的抽样中心，进行正态抽样，得到新的样本点，根据步骤1对样本点进行分析，判断是否落入失效域，计算落入失效域的样本点的失效概率，并将当前f(X)最大值对应的样本点作为第二次抽样的抽样中心。在第q(q＝2,3,…,m)次抽样时，同样根据步骤1对正态抽样得到的样本点进行分析，判断是否落入失效域，计算落入失效域的样本点的失效概率，并比较此次抽样中心的f(Xq)值与当前样本点中最大的f(X)值的大小，若f(Xq)值较大，则取第q次的抽样中心为第q+1的抽样中心，反之，则将当前f(X)最大值对应的样本点作为第q+1次的抽样中心。

第三步：对上述m次抽样得到的失效概率取均值，计算得出复合材料加筋壁板发生后屈曲的失效概率。

具体实施过程：

(1)第1次抽样，即q＝1，选择第1次重要抽样函数为h(1)(X)为正态型，h(1)(X)的抽样中心ΔX(1)为均值点，方差向量与输入向量的联合概率密度函数的方差向量一致，即μh(1)＝μX＝{0.125,0,710,55,25,45,570,1.256×106}T，方差向量按照重要抽样函数h(1)(X)抽取N(1)个样本X(1)s(s＝1,2,…,N(1))，判断样本X(1)s(s＝1,2,…,N(1))是否落入失效域Rn。对于落入Rn区域的抽样点，采用式(7)计算失效概率，并将当前f(X)最大值对应的样本点记为δ*。第2次重要抽样函数为h(2)(X)的抽样中心ΔX(2)即为δ*，方差向量与输入向量的联合概率密度函数的方差向量一致。

(2)第q(q＝2,3,…,m)次的重要抽样密度函数h(q)(X)为正态型，抽样中心为ΔX(q)，方差向量与输入向量的联合概率密度函数的方差向量一致，即μh(q)＝Δx(q)，方差向量按照重要抽样函数h(q)(X)抽取N(q)个样本X(q)s(s＝1,2,…,N(q))，判断样本X(q)s(s＝1,2,…,N(q))是否落入失效域Rn。对于落入Rn区域的抽样点，采用式(7)计算失效概率，并将当前f(X)最大值对应的样本点记为δ*。比较ΔX(q)和δ*对应的联合概率密度函数f(ΔX(q))和f(δ*)的大小；如果f(δ*)≥f(ΔX(q))，则第q+1次的重要抽样密度函数h(q+1)(X)的抽样中心ΔX(q+1)选为δ*；如果f(δ*)＜f(ΔX(q))，则第q+1次的重要抽样密度函数h(q+1)(X)的抽样中心ΔX(q+1)选为ΔX(q)。

(3)进行m次抽样，采用公式(8)计算加筋壁板结构的失效概率算法结束。(为了方便计算m取20，Nq均取100000)

失效概率图如图2所示。由结果可知，相对于传统的蒙特卡洛法，运用自适应抽样法求得的失效概率更快趋于稳定，且自适应抽样方法得到收敛解的模拟次数小于蒙特卡洛法的模拟次数，提高了模拟计算的效率。