技术领域

本发明属于结构可靠性领域，涉及复杂密封结构的可靠性评估方法，具体涉及一种基于Adaboost算法的多失效模式下密封结构可靠性评估方法。

背景技术

密封结构在现代工业领域得到了广泛的应用，密封结构在复杂工况下的失效问题日益凸显。在航空航天领域，飞行器密封结构失效会导致严重后果，造成了很大损失，轻则影响飞行寿命，重则机毁人亡。针对复杂情况下的密封机构失效问题，科研人员做了许多相关研究，以提高密封结构的可靠性。

传统的飞行器密封结构可靠性评估办法一般采用的是有限元计算结合蒙特卡洛模拟的方法。通过有限元仿真来模拟密封结构的失效过程，再直接通过蒙特卡洛方法计算失效概率，进而评估密封结构的可靠性。该方法针对简单的密封结构和单一失效模式取得了良好的效果，但对于多失效模式下的密封结构失效问题则存在着有限元建模复杂，计算时间长，适用范围窄，多失效模式的耦合作用难以模拟等问题。究其原因，在于密封结构失效原因复杂多变。因此对传统的多失效模式下复杂结构可靠性评估办法进行改进是很有必要的。

Adaboost是一种集成学习算法。Adaboost算法的思想是合并多个弱分类器的输出以产生有效的分类。其主要的步骤为:首先给出弱学习算法和样本空间(x,y)，从样本空间中找出m组训练数据,每组训练数据的权重都是然后用弱学习算法迭代运算T次，每次运算后都按照分类结果更新训练数据权重分布，对于分类失败的训练个体赋予较大权重，下一次迭代运算时更加关注这些训练个体。弱分类器通过反复迭代得到一个分类函数序列f1,f2,...,fT，每个分类函数赋予一个权重，分类结果越好的函数,其对应权重越大。T次迭代之后，最终强分类函数F由弱分类函数加权得到。

重要抽样法是一种改进的蒙特卡洛模拟方法。其主要思想是，它不从给定的概率分布函数中进行抽样，而是对所给定的概率分布进行修改，使得对模拟结果有重要贡献的部分多出现，从而达到提高效率，减少模拟的时间，以及缩减方差的目的。

发明内容

要解决的技术问题

为了避免现有技术的不足之处，本发明提出一种基于Adaboost算法的多失效模式下密封结构可靠性评估方法。

技术方案

一种基于Adaboost算法的多失效模式下密封结构可靠性评估方法，其特征在于步骤如下：

步骤1：构造训练样本和测试样本

将实验过程中O型密封圈的弹性模量、泊松比、油压和预压缩量作为特征，在同一载荷谱中运行105小时后结构是否失效作为二分类标签，制作出样本容量为N的实验样本；其中，输入的各个参数互相独立且可近似认为服从正态分布，随机抽取80％作为训练样本，其余20％作为测试样本；

步骤2：运用Adaboost算法对训练样本进行分类

采用matlab工具箱中的adaboostM1二分类算法，弱学习器类型为决策树，对训练样本进行分类进行多轮训练；将训练好的分类模型记作F(X)，其中X为O型圈的输入特征向量，若F(X)<0，则认定在该输入条件下，O型密封圈失效；否则认定O型密封圈未失效；

步骤3：采用重要抽样法计算失效概率

采取扩大方差的重要抽样法来计算O型密封圈的失效概率，扩大系数设为1.05，抽取N组数据，记作Xi，i＝1，2，…,N，代入训练好的分类模型F(X)，当F(Xi)<0时，认定在Xi下O型密封圈失效；

利用计算失效概率，式中i为使F(Xi)<0成立的所有可能值；gcov为扩大方差后设计参数的联合概率密度分布函数；fcov为扩大方差前设计参数的联合概率密度分布函数。

有益效果

本发明提出的一种基于Adaboost算法的多失效模式下密封结构可靠性评估方法，采用Adaboost算法对小样本的密封圈失效相关数据进行分类迭代训练，直至集合分类器的分类误差达到精度要求，然后采用重要抽样法来计算密封结构相关参数波动情况下的失效概率，进而评估多失效模式下密封结构的可靠性。本发明解决了复杂结构多失效模式下可靠性评估耗时久，计算过程复杂的难题，对多失效模式下的复杂结构可靠性评估和设计优化问题具有重要的指导意义和实践价值。

附图说明

图1训练数据分布图

图2分类器h1数据分类

图3分类器h2数据分类

图4分类器h3数据分类

图5分类器整合分类

图6重要抽样法示意图

图7训练次数与误差的关系图

具体实施方式

现结合实施例、附图对本发明作进一步描述：

1)Adaboost集成网络分类原理

下面以多失效模式下的密封结构为例，阐述采用Adaboost分类的原理和收敛性证明。

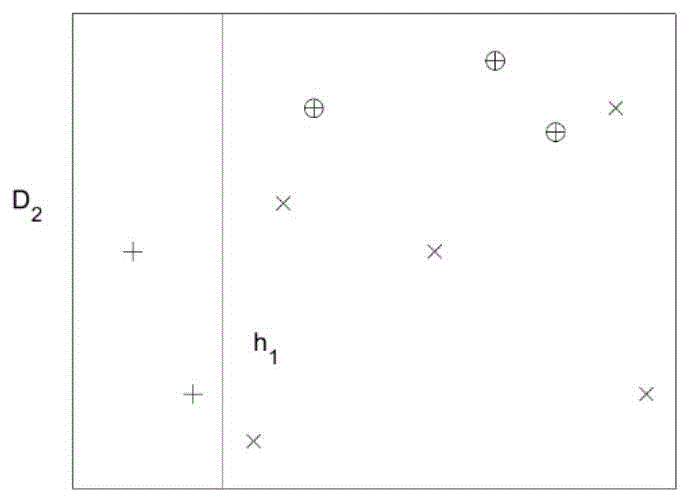
在图1中，训练数据集中“+”和“x”分别代表结构不失效或失效这两个类别。D1是当前数据的分布。理论上每一种失效模式都对应着一条描述极限状态方程的曲线，这些曲线将训练数据分为失效和不失效两个类别。但由于目前对失效机理的研究不足和失效模式的相互耦合难以模拟，我们无法通过解析方法或有限元方法得到准确的失效域和安全域的边界曲线。

我们可以通过Adaboost算法来找到最优的分类方法。按照Adaboost算法的思想需要构建多个简单的分类器，然后分类器加和的结果作为最终的分类器。

第一步，找到第一个分类器h1，如图2所示。算法初始给了一个均匀分布D。所以h1中每个点的权重是0.1。当划分后，有三个点划分错了(图2中画圆圈的样本)，根据算法误差表达式得到的误差为分错了的三个点的权值之和，所以ε1＝0.1+0.1+0.1＝0.3，而α1的值由式(1)给出：

由上式可知，当εt≤1/2时，αt≥0，且αt随着εt的减小而增大，意味着分类误差率越小的分类器的基本分类器在最终分类器中的作用越大。通过此方法，Adaboost算法能重点关注那些难以分辨的样本。

第二步，根据算法将分错点得权值变大。对于分对的七个点，它们的权值减小。对于分错的三个点，其权值由下面所给出的计算公式求得：

式中，表示第t轮的样本权重系数，αt为第t轮分类器的加和系数，yi为样本的实际分类结果，Gt(xi)表示第t轮的分类器。

因为α＞0，所以分类样本的权重会变大，相应的分对样本的权重减少。这样就得到了新的权重分布。

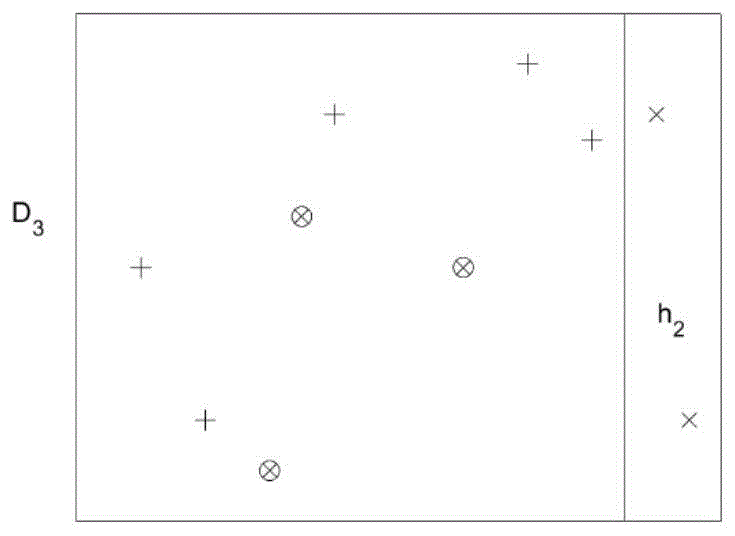
第二步，根据分布D2，得到一个新的子分类器h2和更新后的样本分布D3,如图3所示。

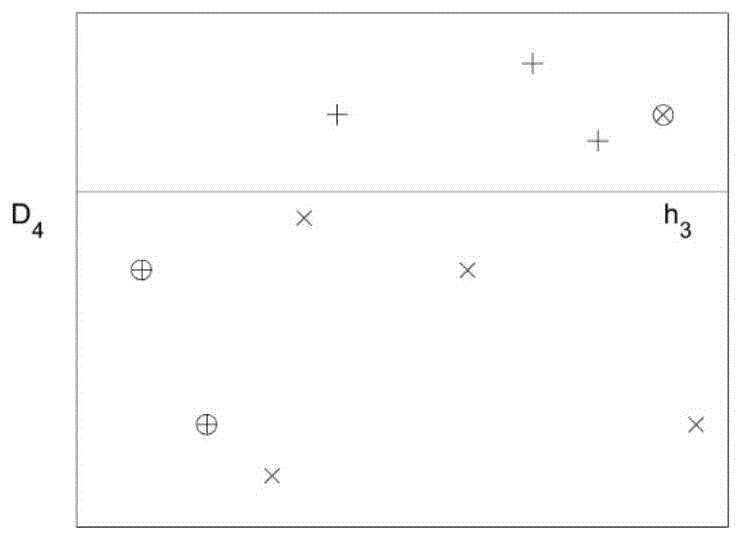
第三步，根据分布D3,得到一个新的子分类器h3，如图4所示。

各子分类器误差和权值计算结果如表1所示。

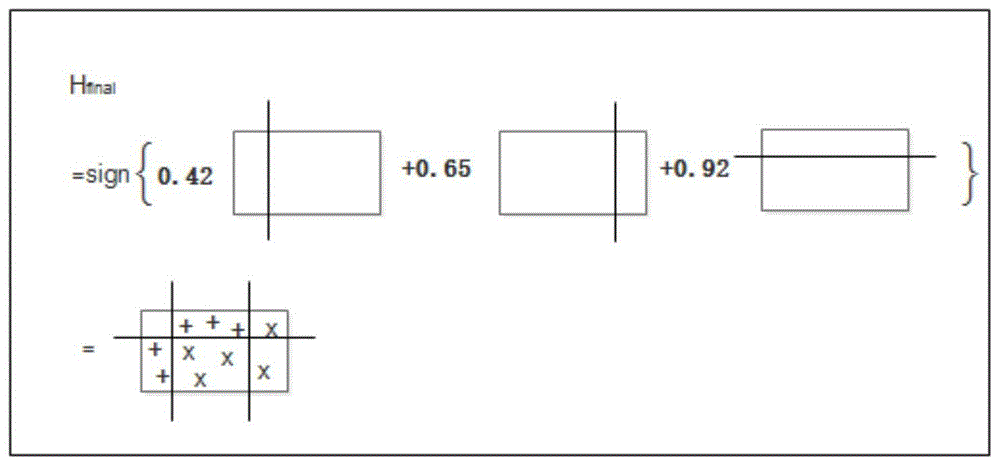
表1.子分类器误差及权值

子分类器 h1 h2 h3 误差et 0.3 0.21 0.14 权值αt 0.42 0.65 0.92

整合所有子分类器，如图5所示。

从图5所示，通过这些简单的分类器，最终即使对于一个线性不可分的数据集，也能得到很低的错误率。

2)采用重要抽样法计算失效概率

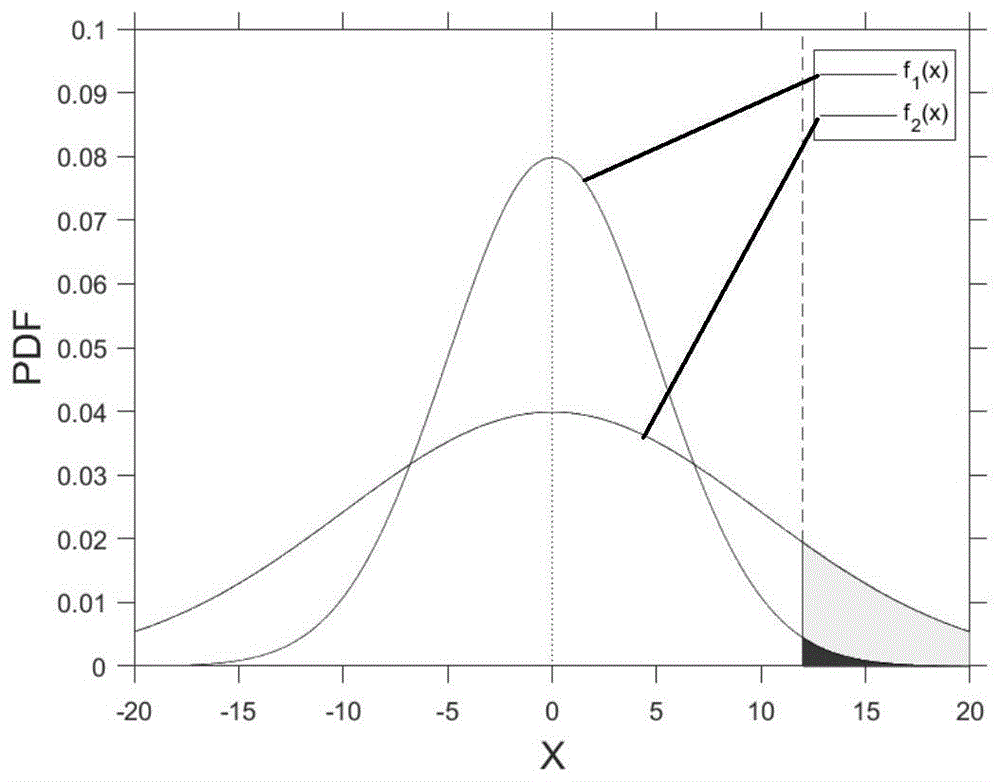
本发明采用的是基于扩大方差的重要抽样方法。通过扩大抽样样本的方差，来提高失效点在样本中出现的频率，从而提高抽样效率。如图6所示，f1(x)为样本的概率密度分布函数，红色部分为失效域；f2(x)为样本扩大方差后的概率密度分布函数，黄色部分加红色部分为失效域。可以明显看出当失效概率极小的时候，如果采用蒙特卡洛方法，抽样次数需要极大才能保证失效概率的计算精度，而采用基于方差的重要抽样法需要的抽样次数相较于蒙特卡洛法有相当程度的减少，在保证计算精度的同时大大提高了计算效率。对于结构优化设计问题，工程师需要快速评估改变结构的相关参数对结构失效概率的影响。采用基于扩大方差的重要抽样法来计算失效概率可以显著提高计算速度。基于方差的重要抽样法计算公式如下：

式中，N为抽样次数，为扩大方差样本的第i次失效判别通过的样本点的联合概率分布函数，为扩大方差样本第i次失效判别通过的样本点对应的原样本的联合概率分布函数。

具体步骤如下：

步骤1：构造训练样本和测试样本

我们将实验过程中O型密封圈的弹性模量，泊松比，油压，预压缩量作为特征，在同一载荷谱中运行105小时后结构是否失效作为二分类标签，制作出样本容量为2000的实验样本。其中，输入的各个参数互相独立且可近似认为服从正态分布。随机抽取1600组数据作为训练样本，其余400组作为测试样本。

步骤2：运用Adaboost算法对训练样本进行分类

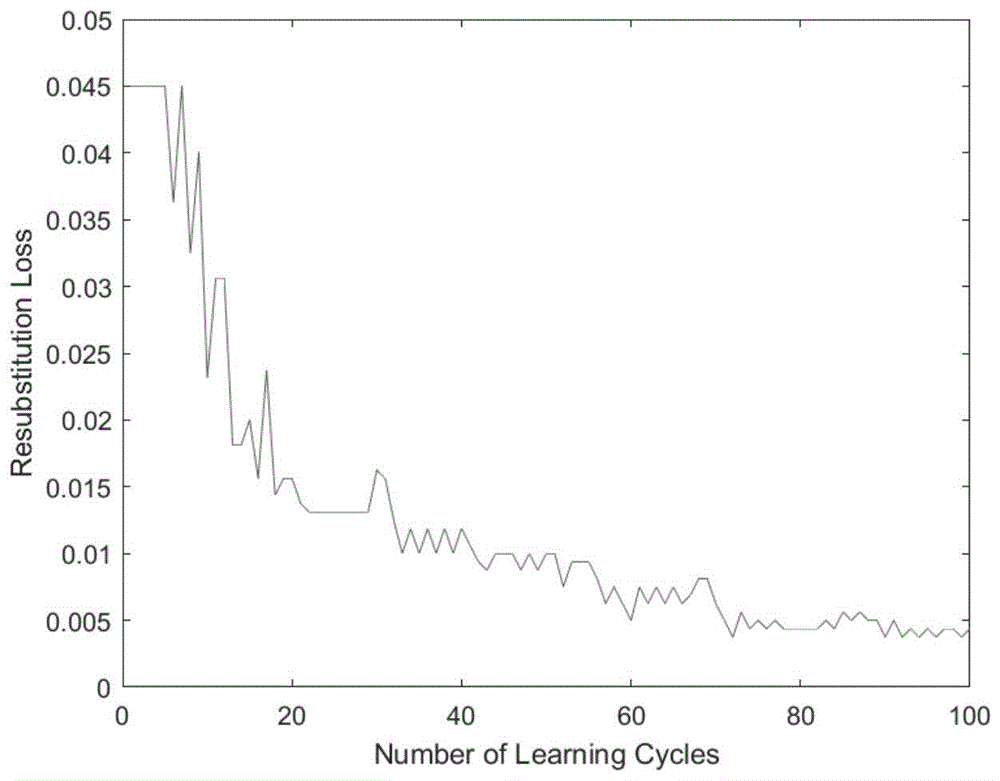
采用matlab工具箱中的adaboostM1二分类算法，弱学习器类型为决策树，训练100轮。训练次数与误差的关系图如图7所示。

可以看出，随着训练轮数的增加，训练模型的误差收敛于一个极小值。

我们将训练好的分类模型记作F(X),X为O型圈的输入特征向量。若F(X)<0，则认定在该输入条件下，O型密封圈失效；否则认定O型密封圈未失效。

利用训练得到的模型可以预测400组测试样本数据的分类标签，和有限元分析结果进行比对，求得分类误差率为：error＝1.75％。与传统的有限元仿真方法相比，Adaboost分类模型大大提高了临界状态下样本的失效判别准确率。

步骤3：采用重要抽样法计算失效概率

我们需要对工程师提出的O型密封圈结构新的设计进行可靠性评估。参数如表2所示。

表2.设计参数

设计参数 密封圈弹性模量 密封圈泊松比 预压缩量 油压 均值 13.4 0.398 -0.8 5.34 标准差 0.268 0.00796 0.024 0.1068

为了进一步提高计算效率，我们采取扩大方差的重要抽样法来计算O型密封圈的失效概率。扩大系数设为1.05，抽取2000组数据，记作Xi(i＝1，2，…,2000)，代入训练好的分类模型F(X)，当F(Xi)<0时，认定在Xi下O型密封圈失效。

利用计算失效概率，式中i为使F(Xi)<0成立的所有可能值；gcov为扩大方差后设计参数的联合概率密度分布函数；fcov为扩大方差前设计参数的联合概率密度分布函数。求得失效概率Pf＝0.00034。

如果直接采用蒙特卡罗方法调用有限元计算，要达到失效概率估计值的变异系数为0.1的要求，需要调用有限元模型2.9×105次以上，有限元模型计算一次约3分钟，预估耗时14500小时，约604天；本发明采用基于Adaboost算法与重要抽样法联合分析，仅需调用有限元2000次以得到训练样本，从而计算Adaboost集成算法参数，再计算失效概率，全程耗时约16小时。可以看出，所提出的可靠性评估方法在计算速度上相较于传统方法具有显著优势。

本发明采用adaboost算法对密封结构的训练数据不断进行简单分类，然后整合成为一个准确率极高的集成分类器。通过基于扩大方差的重要抽样方法，将抽样得到的样本带入训练好的分类器进行判别，从而计算出密封结构的失效概率。与传统可靠性评估办法相比，该方法调用有限元模型的次数大大减少，计算效率显著提高，缩短了计算所需时间。该发明提出了一种合理，便捷的复杂结构多失效模式失效概率计算方法，为设计者针对复杂结构进行可靠性评估和优化设计奠定了基础。