技术领域

本发明涉及飞机结构设计领域，尤其是一种灵敏度分析方法。

背景技术

翼盒是飞机机翼的主要承力结构，主要由前梁、后梁、内部翼肋、上下壁板组成，翼盒作为外翼结构中最主要的承力部件，对整个机翼有着重要的影响。翼盒前端连接固定前缘和前缘缝翼，后端连接副翼、襟翼和扰流板，下端连接发动机吊挂和起落架。飞机运营过程中所有工作情况下的载荷都会传递到翼盒上，这就需要对翼盒结构的传力路线、几何结构做出较好的设计。在机翼的详细设计阶段，结构形式以及布局已经确定，机翼在飞机飞行过程中产生升力，是飞机能够飞行的根本保障。翼盒的结构设计，对机翼甚至整个飞机的影响有着至关重要的作用。好的结构设计不仅能够保证机翼产生正常的气动升力，以及机翼内系统的正常运作，而且能够充分发挥材料的性能优势，减轻结构重量，提高结构可靠性。参数灵敏度分析可以了解变量对结构可靠性的相对重要程度，从而为结构分析和优化设计提供参考。目前，概率可靠性分析方法已经应用较为充分，与之相应的基于概率模型下的参数灵敏度分析也日渐成熟。基于概率模型的参数灵敏度分析需要认定参数是随机变量，并有参数的分布规律、均值、方差等信息。而在结构设计过程中，缺乏充足的信息来确定结构设计参数的分布规律、均值、方差、概率密度函数等信息，限制了基于概率模型的参数灵敏度分析方法的应用。

非概率模型能有效地解决数据量较少、变量概率密度函数缺失情况下等可靠性问题而备受关注。20世纪90年代以来，基于凸集模型的非概率可靠性的概念被提出，并提出以系统能容许的不确定性的最大程度度量可靠性。总的来说，非概率的凸集模型可分为区间模型和椭球模型两种。相比于区间模型，椭球模型能描述多个不确定变量之间的相关性，当变量不相关时，椭球模型退化成区间模型，由此可知，区间模型可视为椭球模型的特例。目前，针对椭球模型的结构可靠性分析已有较为深入的研究，而基于椭球模型的结构参数灵敏度问题亟待解决。

发明内容

为了克服现有技术的不足，本发明针对飞机机翼翼盒结构设计参数信息不充足的情况，提出一种基于椭球模型下的结构参数灵敏度分析方法，对于结构功能函数为线性的情况，推导出了结构参数灵敏度的解析解。

本发明解决其技术问题所采用的技术方案的详细步骤如下：

步骤1：设飞机机翼翼盒结构的功能函数为g(x)，x为结构参数，是一个n维变量，记为x＝(x1,x2,…,xi,…,xn)，xi为第i个结构参数，满足于椭球模型U(u,σ)，U(u,σ)如下所示：

其中，u＝(u1,u2,…ui,…,un)为椭球模型U(u,σ)的位置参数，σ＝(σ1,σ2,…,σi,…,σn)为椭球模型U(u,σ)的尺寸参数，i＝1,2,…,n，ui为椭球模型U(u,σ)的第i个位置参数，σi为椭球模型U(u,σ)的第i个尺寸参数；

步骤2：当功能函数g(x)等于0时，其形成的曲面g(x)＝0将变量空间分为安全域Ds(x:g(x)＞0)和失效域Df(x:g(x)＜0)，结构的可靠性指标η表示为式(2)：

其中，λ为尺寸参数的比例因子；

求解得到可靠性指标η和优化解x*，其中x*为g(x)＝0对应的设计点；

步骤3：由于概率模型下结构参数灵敏度定义为失效概率Pf对基本变量分布参数θx的偏导数，即同理，基于椭球模型U(u,σ)下结构的参数灵敏度定义为椭球模型下可靠性指标η对其参数的偏导数，即可靠性指标η对椭球模型U(u,σ)中的位置参数u和尺寸参数σ的偏导数，分别用和表示；

当机翼翼盒结构的功能函数g(x)为线性函数时，功能函数g(x)如下所示：

其中，x满足式(1)，a0是常数项，bi为功能函数g(x)中的系数；

定义中间变量z＝(z1,z2,…,zi,…,zn)，zi＝(xi-ui)/σi，则中间变量z为n维单位超球体，即

将zi代入到式(3)，则功能函数g(x)改写为：

由于g(z)是线性函数，得到椭球模型U(u,σ)下结构的可靠性指标η为:

则对于机翼翼盒结构功能函数g(x)形式如式(3)所示时，基于椭球模型U(u,σ)的结构参数灵敏度的解析式为：

由此可得椭球模型U(u,σ)的结构参数灵敏度。

本发明的有益效果在于由于定义了椭球模型下的机翼翼盒结构参数的灵敏度指标，推导机翼翼盒结构功能函数为线性情况下参数灵敏度的解析求解方法，以机翼九盒段结构灵敏度分析，证明了解析方法的正确性和有效性，本发明的分析结果对机翼翼盒结构的可靠性分析和结构改设计有着重要的意义。

附图说明

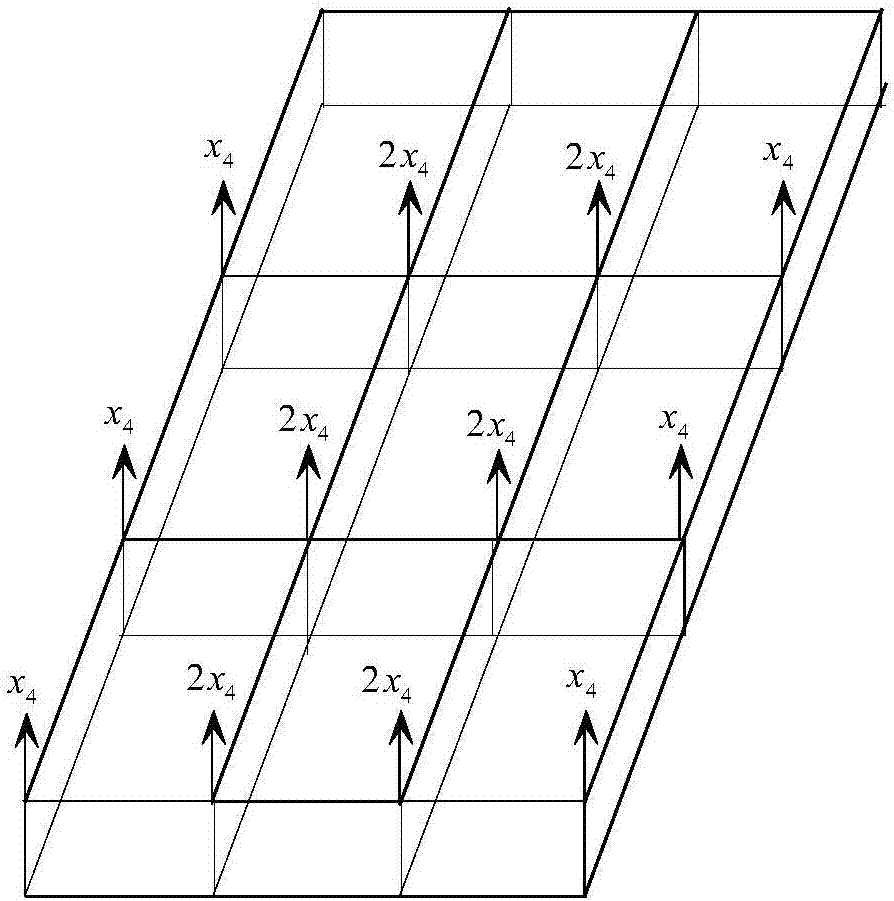
图1为本发明飞机机翼九盒段结构示意图，其中x4和2x4为机翼九盒段结构节点处所施加的负荷。

具体实施方式

下面结合附图和实施例对本发明进一步说明。

步骤1：设飞机机翼翼盒结构的功能函数为g(x)，x为结构参数，是一个n维变量，记为x＝(x1,x2,…,xi,…,xn)，xi为第i个结构参数，为满足于椭球模型U(u,σ)，U(u,σ)如下所示：

其中，u＝(u1,u2,…ui,…,un)为椭球模型U(u,σ)的位置参数，σ＝(σ1,σ2,…,σi,…,σn)为椭球模型U(u,σ)的尺寸参数，i＝1,2,…,n，ui为椭球模型U(u,σ)的第i个位置参数，σi为椭球模型U(u,σ)的第i个尺寸参数；

步骤2：当功能函数g(x)等于0时，其形成的曲面g(x)＝0将变量空间分为安全域Ds(x:g(x)＞0)和失效域Df(x:g(x)＜0)，结构的可靠性指标η表示为式(2)：

其中，λ为尺寸参数的比例因子；

从式(2)看出，基于椭球模型的结构可靠度指标η的求解实际上是一个带约束的优化问题，通过模拟退火优化方法或者遗传算法，求解得到可靠性指标η和优化解x*，其中x*为g(x)＝0对应的设计点；

步骤3：由于概率模型下结构参数灵敏度定义为失效概率Pf对基本变量分布参数θx的偏导数，即同理，基于椭球模型U(u,σ)下结构的参数灵敏度定义为椭球模型下可靠性指标η对其参数的偏导数，即可靠性指标η对椭球模型U(u,σ)中的位置参数u和尺寸参数σ的偏导数，分别用和表示；

当机翼翼盒结构的功能函数g(x)为线性函数时，功能函数g(x)如下所示：

其中，x满足式(1)，a0是常数项，bi为功能函数g(x)中的系数；

定义中间变量z＝(z1,z2,…,zi,…,zn)，zi＝(xi-ui)/σi，则中间变量z为n维单位超球体，即

将zi代入到式(3)，则功能函数g(x)改写为：

由于g(z)是线性函数，得到椭球模型U(u,σ)下结构的可靠性指标η为:

则对于机翼翼盒结构功能函数g(x)形式如式(3)所示时，基于椭球模型U(u,σ)的结构参数灵敏度的解析式为：

由此可得椭球模型U(u,σ)的结构参数灵敏度。

图1中显示了由64杆和42板元件组成的机翼九盒段结构，结构材质为铝合金，结构单元的强度(x1,x2,x3)和所施加的负荷(x4)为变量。结构体系的主要失效模式用最优准则法来获得，并进行变量(x1,x2,x3,x4)单位的归一化处理，最终得到的功能函数g(x)如式(8)所示：

g(x)＝4.0x1+4.0x2-3.9998x3-x4 (8)

当g(x)＞0，结构安全；当g(x)＜0，结构失效。九盒段结构的变量x1,x2,x3,x4满足椭球模型U(u,σ)如式(9)所示。

椭球模型U(u,σ)下机翼九盒段结构参数变量的位置参数和尺寸参数值如表1所示：

表1

基于椭球模型U(u,σ)的机翼九盒段结构参数灵敏度计算的结果如表2所示：

表2

本实施例分析了机翼九盒段结构的参数灵敏度，如表2所示，将有限差分法作为验证解，两种方法所得结果的差异小于1％，这表明本发明提出的方法对于解决机翼翼盒结构线性功能函数情况时，基于椭球模型下的参数灵敏度问题是有效可行的。