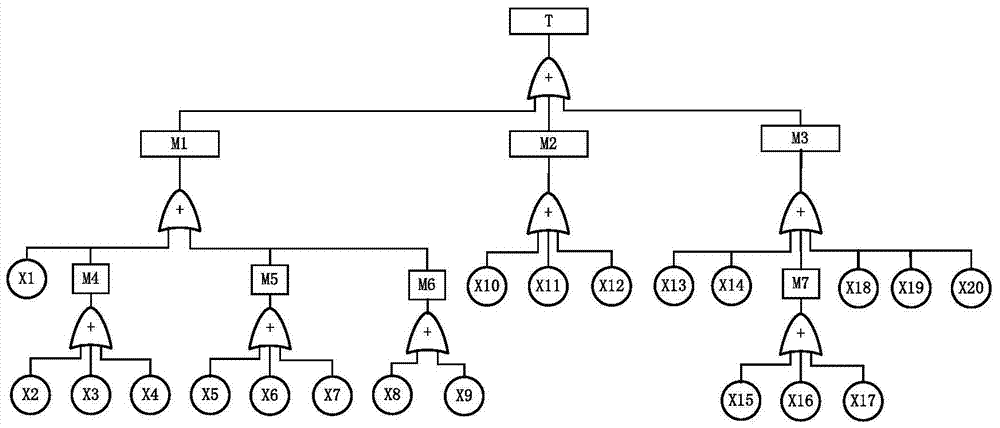
1.一种飞机起落架收放系统在小样本、贫信息下的可靠性评估方法,其特征在于步骤如下:步骤1:基于系统原理和故障机理,建立飞机起落架收放系统故障树,所述的飞机起落架收放系统故障树各层逻辑关系:X2、X3和X4构成或门逻辑树到M4,X5、X6和X7构成或门逻辑树到M5,X8和X9构成或门逻辑树到M6,X15、X16和X17构成或门逻辑树到M7;X1、M4、M5和M6构成或门逻辑树到M1,X10、X11和X12构成或门逻辑树到M2,X13、X14、M7、X18、X19、X20构成或门逻辑树到M3;M1、M2和M3构成或门逻辑树到T;其中,M1-作动筒异常、M2-控制系统异常、M3-液压系统异常、X2-活塞杆卡滞、X3-活塞杆松动、X4-活塞杆断裂、X5-密封圈机械损坏、X6-密封圈老化龟裂、X7-密封圈化学腐蚀、X8-耳环螺栓断裂、X9-耳环转动、X15-泵柱赛弹簧断裂、X16-泵旋转接头漏油、X17-泵电机损坏、X1-作动筒断裂、M4-活塞杆异常、M5-密封圈异常、M6-端头耳环异常、X10-压力开关失效、X11-电磁开关失效、X12-安全活门失效、X13-液压管路漏油、X14-气塞、X18-油液污染、X19-硬导管破裂、X20-蓄压器破裂、M7-液压泵异常、T-起落架收放系统异常;步骤2:基于区间与泛灰的转换规则,将飞机起落架收放系统故障树各底事件X1~X20的失效概率区间形式转化为泛灰数表示形式其中,为Xi的失效概率下限,为Xi的失效概率上限;步骤2:建立单层的基于泛灰模型的故障树逻辑或门算子根据故障树的层与层之间的逻辑关系建立从底事件到顶事件的飞机起落架缓冲系统失效传递函数XTOP=f(X1,X2,...,X20);步骤3:使用泛灰四则运算法则对飞机起落架缓冲系统失效传递函数XTOP=f(X1,X2,...,X20)计算得到顶事件失效概率泛灰形式基于区间与泛灰的转换规则,将顶事件失效概率泛灰形式转换为区间形式从而得到基于泛灰算法的飞机起落架缓冲系统失效概率范围,根据飞机起落架缓冲系统失效概率范围对发生故障进行可靠性评估;其中,为飞机起落架缓冲系统失效概率的下限,为飞机起落架缓冲系统失效概率的上限。
2.根据权利要求1所述的一种飞机起落架收放系统在小样本、贫信息下的可靠性评估方法,其特征在于所述的泛灰四则运算法则为:设则有:其中,x1、x2为观测值,分别为x1、x2的灰信息部。
技术领域
本发明涉及到小样本、贫信息下飞机起落架收放系统的可靠性分析,基于泛灰算法进行系统故障树分析,来获得系统更为精确的可靠度,从而对系统的安全程度进行评估。
背景技术
近年来,各类大型复杂系统所使用的技术越来越先进、其内部结构越来越复杂,自动化程度越来越高,则系统运行的安全性和可靠性便越来越受到人们的重视。起落架作为飞机的起飞着陆装置,主要用于飞机的起飞、着陆、地面滑跑和地面停放。为了减小飞行阻力,现代飞机的起落架通常是可收放的,而起落架收放系统的作用便是保证飞机在起飞后将起落架顺利收入机身内部并关闭起落架舱,着陆前再放下起落架,将之固定在一定的位置并锁住。相关数据显示,近年来飞机发生的飞行故障中15%是由于飞机起落架故障导致的,而在起落架故障中,又有23%是由于起落架收放系统故障导致的。2007年,俄罗斯一架图-134客机在机场着陆时由于飞机起落架出现故障无法打开,飞行员最终只好用机身擦地迫降,造成严重事故;2009年,一架津巴布韦籍货机在上海浦东国际机场坠落,起飞时主起落架没有收起,起飞速度不够坠毁。美国海军陆战队的一架AV-8B垂直起降战斗机在放不下起落架的情况下进行迫降,飞机受损严重;2007年,北京至迪拜航线的一架波音客机前部起落架突然意外收起,飞机机头和部分机腹前倾着地,导致机上多名人员摔倒受伤。可见飞机起落架收放系统工作性能的好坏直接影响着飞机的起飞、着陆性能和飞机的安全,轻者飞机受损,重者机毁人亡,造成巨大的经济损失和人员伤亡。究其原因,起落架收放系统本身结构较为复杂,在设计环节很难做到充分认识,同时由于成本因素,后期试验样本有限,因而普遍呈现小样本、贫信息特点。因此,对类似于失效统计信息缺乏的起落架系统这样的大型复杂系统进行可靠性评估,保障飞机的飞行安全,避免灾难性事故的发生,减少人员和财产的损失,具有重要的现实意义。
作为系统可靠性评估的主要方法,故障树分析法通过系统底层部件的失效概率统计,同时基于系统原理和故障机理得到系统各层部件之间的逻辑关系,层层推导得到系统顶层失效概率,从而达到系统级的可靠性评估。
目前针对系统可靠性的故障树分析主要形成了基于随机模型和区间模型两大类方法。基于随机模型的系统故障树分析通过大量系统失效统计数据得到底事件较为精确的失效概率描述,结合故障树与或门逻辑关系最终得到顶事件失效概率,并在此过程中逐渐建立了以抽样法、近似算法和不交化求解方法为代表的针对故障树顶事件失效概率和底事件重要度的改进方法;基于区间模型的系统故障树分析以区间域的形状来反映对事件的已知程度,以大小来反映不确定事件的波动性或偏离程度,结合故障树与或门逻辑关系和区间运算法则层层推导得到顶事件失效概率。
但需要指出的是,基于随机模型的故障树分析法虽然发展已较为成熟,但其结果的精确性对数据量要求较为敏感,适用于对失效统计数据较为充足下的一类系统进行可靠性分析,难以解决小样本、贫信息系统的可靠性评估问题;虽然区间模型仅需要不确定事件集合的界限,而不需要确定其内部分布情况,因而对数据的依赖性明显低于随机模型,但在基于区间运算进行系统顶事件失效概率范围求解过程中,由于区间运算本身存在的缺陷,即同一个表达式由于运算次序不同而导致解区间被放大或缩小的问题,使得基于区间运算得到的系统失效概率难以具有较强的参考价值。以具有两个底事件的故障树或门区间算子为例,其顶事件失效概率表达式为PTop=1-(1-p1)(1-p2),化简后为PTop=p1+p2+p1p2,若赋值p1=[0.1,0.3]和p2=[0.4,0.8]并代入进行区间运算求解,发现前者表达式结果为[0.46,0.86],而后者结果为[0.26,1.06]。
发明内容
要解决的技术问题
克服随机模型对数据量要求较高、区间模型由于运算次序不同而导致解区间被放大或缩小的问题,从而实现起落架收放系统在小样本、贫信息下更为精确的可靠性评估。
技术方案
一种飞机起落架收放系统在小样本、贫信息下的可靠性评估方法,其特征在于步骤如下:
步骤1:基于系统原理和故障机理,建立飞机起落架收放系统故障树,所述的飞机起落架收放系统故障树各层逻辑关系:X2、X3和X4构成或门逻辑树到M4,X5、X6和X7构成或门逻辑树到M5,X8和X9构成或门逻辑树到M6,X15、X16和X17构成或门逻辑树到M7;X1、M4、M5和M6构成或门逻辑树到M1,X10、X11和X12构成或门逻辑树到M2,X13、X14、M7、X18、X19、X20构成或门逻辑树到M3;M1、M2和M3构成或门逻辑树到T;
其中,X2-活塞杆卡滞、X3-活塞杆松动、X4-活塞杆断裂、X5-密封圈机械损坏、X6-密封圈老化龟裂、X7-密封圈化学腐蚀、X8-耳环螺栓断裂、X9-耳环转动、X15-泵柱赛弹簧断裂、X16-泵旋转接头漏油、X17-泵电机损坏、X1-作动筒断裂、M4-活塞杆异常、M5-密封圈异常、M6-端头耳环异常、X10-压力开关失效、X11-电磁开关失效、X12-安全活门失效、X13-液压管路漏油、X14-气塞、X18-油液污染、X19-硬导管破裂、X20-蓄压器破裂、M7-液压泵异常、T-起落架收放系统异常;
步骤2:基于区间与泛灰的转换规则,将飞机起落架收放系统故障树各底事件X1~X20的失效概率区间形式转化为泛灰数表示形式其中,pi为Xi的失效概率下限,为Xi的失效概率上限;
步骤2:建立单层的基于泛灰模型的故障树逻辑或门算子根据故障树的层与层之间的逻辑关系建立从底事件到顶事件的飞机起落架缓冲系统失效传递函数XTOP=f(X1,X2,...,X20);
步骤3:使用泛灰四则运算法则对飞机起落架缓冲系统失效传递函数XTOP=f(X1,X2,...,X20)计算得到顶事件失效概率泛灰形式基于区间与泛灰的转换规则,将顶事件失效概率泛灰形式转换为区间形式从而得到基于泛灰算法的飞机起落架缓冲系统失效概率范围,根据飞机起落架缓冲系统失效概率范围对发生故障进行可靠性评估;其中,pTOP为飞机起落架缓冲系统失效概率的下限,为飞机起落架缓冲系统失效概率的上限。
所述的泛灰四则运算法则为:
其中,x1、x2为观测值,分别为x1、x2的灰信息部。
有益效果
本发明提出的一种基于泛灰算法的故障树分析方法,能够实现针对起落架收放系统各部件失效统计信息不充足即小样本、贫信息下的系统可靠性评估。
附图说明
图1 飞机起落架收放系统故障树
T—起落架收放系统异常;M1—作动筒异常;M2—控制系统异常;M3—液压系统异常;M4—活塞杆异常;M5—密封圈异常;M6—端头耳环异常;M7—液压泵异常;X1—作动筒断裂;X2—活塞杆卡滞;X3—活塞杆松动;X4—活塞杆断裂;X5—密封圈机械损坏;X6—密封圈老化龟裂;X7—密封圈化学腐蚀;X8—耳环螺栓断裂;X9—耳环转动;X10—压力开关失效;X11—电磁开关失效;X12—安全活门失效;X13—液压管路漏油;X14—气塞;X15—泵柱赛弹簧断裂;X16—泵旋转接头漏油;X17—泵电机损坏;X18—油液污染;X19—硬导管破裂;X20—蓄压器破裂。
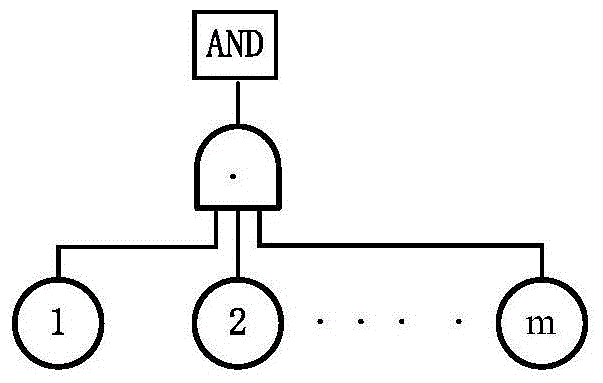
图2 逻辑与门符号
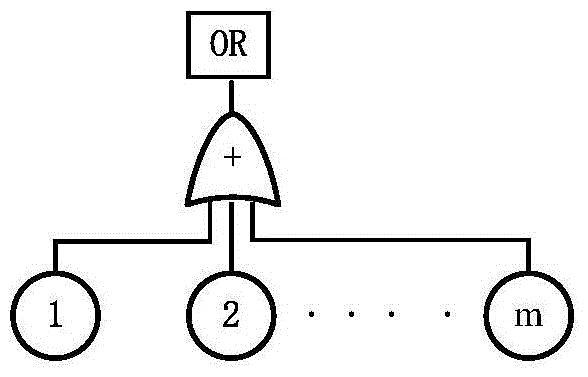
图3 逻辑或门符号
具体实施方式
现结合实施例、附图对本发明作进一步描述:
根据起落架收放系统工作原理、组成结构、故障分类等,构建系统故障树,如图1所示;
如表1所示,同时给出了起落架收放系统故障树各底事件的失效概率区间如下:
表1 起落架收放系统故障树底事件失效概率区间
令“*”,*∈{+,-,·,/}表示实数集上的实二元运算。对任意定义区间数集I(R)上的二元运算如下:
[x]*[y]={z|z=x*y,x∈[x],y∈[y]} (1)
则有下列四则运算法则:
设论域U=R(实数集),则称R上的泛灰集为泛灰数集,记作g(R)且称g(R)中的元素为泛灰数,记作:x∈R,式中,x为观测值,为x的灰信息部。
则有如下四则运算法则:
在实际应用中,泛灰数和区间数可以相互转化,若已知泛灰数则其对应的区间数形式为若已知区间数为了方便运算,可将其统一表示为形式。将故障树中各底事件失效概率区间依次表示为基于区间与泛灰的转换规则,将故障树各底事件失效概率区间形式统一转化为泛灰数表示形式如表2所示;
表2 起落架收放系统故障树底事件失效概率泛灰表示
在故障树逻辑与门中,当所有底事件i(i=1~n)都发生时,顶事件“AND”发生,泛灰模型下的与门算子为在故障树逻辑或门中,当至少有一个底事件i(i=1~n)发生时,顶事件“OR”发生,泛灰模型下的或门算子为其中与、或门逻辑符号如图2、3所示:
基于故障树与或门逻辑关系,得到起落架收放系统故障树结构函数如下:
T=1-(1-PM1)(1-PM2)(1-PM3) (7)
泛灰运算过程如下:
PM4=1-(1-PX2)(1-PX3)(1-PX4)
=(1,[1,1])-{(1,[1,1])-(9.29×10-5,[0.282024,1])}·{(1,[1,1])-(1.40×10-4,[0.458571,1])}
·{(1,[1,1])-(8.85×10-6,[0.237288,1])}
=(2.4×10-4,[0.3793,1])
PM5=1-(1-PX5)(1-PX6)(1-PX7)
=(1,[1,1])-{(1,[1,1])-(2.45×10-3,[0.187755,1])}·{(1,[1,1])-(8.29×10-4,[0.316043,1])}
·{(1,[1,1])-(9.72×10-4,[0.251029,1])}
=(4.246×10-3,[0.227505,1])
PM6=1-(1-PX8)(1-PX9)
=(1,[1,1])-{(1,[1,1])-(1.95×10-3,[0.235897,1])}·{(1,[1,1])-(7.29×10-4,[0.307270,1])}
=(2.678×10-3,[0.2555464,1])
PM7=1-(1-PX15)(1-PX16)(1-PX17)
=(1,[1,1])-{(1,[1,1])-(1.85×10-4,[0.248649,1])}·{(1,[1,1])-(7.52×10-4,[0.324468,1])}
·{(1,[1,1])-(7.72×10-3,[0.317358,1])}
=(8.65×10-3,[0.3167134,1])
由此可求得:
PM1=1-(1-PX1)(1-PM4)(1-PM5)(1-PM6)
=(1,[1,1])-{(1,[1,1])-(6.40×10-5,[0.315625,1])}·{(1,[1,1])-(2.4×10-4,[0.3793,1])}
·{(1,[1,1])-(4.246×10-3,[0.227505,1])}·{(1,[1,1])-(2.678×10-3,[0.2555464,1])}
=(7.2145×10-3,[0.2431464,1])
PM2=1-(1-PX10)(1-PX11)(1-PX12)
=(1,[1,1])-{(1,[1,1])-(8.29×10-5,[0.195416,1])}·{(1,[1,1])-(8.09×10-4,[0.264524,1])}
·{(1,[1,1])-(1.44×10-3,[0.343750,1])}
=(2.33×10-3,[0.310623,1])
PM3=1-(1-PX13)(1-PX14)(1-PM7)(1-PX18)(1-PX19)(1-PX20)
=(1,[1,1])-{(1,[1,1])-(7.20×10-3,[0.363889,1])}·{(1,[1,1])-(8.25×10-4,[0.317576,1])}
·{(1,[1,1])-(8.65×10-3,[0.3167134,1])}·{(1,[1,1])-(9.85×10-3,[0.283249,1])}
·{(1,[1,1])-(8.29×10-5,[0.255730,1])}·{(1,[1,1])-(1.70×10-4,[0.260000,1])}
=(2.65324×10-2,[0.318568,1])
最终得到:
T=1-(1-PM1)(1-PM2)(1-PM3)
=(1,[1,1])-{(1,[1,1])-(7.2145×10-3,[0.2431464,1])}·{(1,[1,1])-(2.33×10-3,[0.310623,1])}
·{(1,[1,1])-(2.65324×10-2,[0.318568,1])}
=(0.0358,[0.3044832,1])
=[0.0109,0.0358]
由此可以得到,飞机起落架收放系统的失效概率范围在0.0109~0.0358之间。可见,在表1中所给出的系统各部件失效概率区间值之下,100次的飞机起落架收起、放下过程中,会有1~3次发生故障,从而实现了对起落架收放系统功能安全程度的量化评估。


评论
全部评论
共{{commentCount}}条{{rs.Msg_Content}}