技术领域

本发明属于通信技术领域，具体涉及一种Mesh网关部署优化方法。

背景技术

在现在5G网络的迅速发展过程中，物联网，被视为继互联网之后的又一次资讯技术革命浪潮，在万物互联的世界中，无线Mesh网络的重要性越来越突出。同时在无线Mesh网络多网关特征中，网关部署优化算法至关重要，直接影响到整个网络的服务质量，如何进行有效的部署网关，可以最大程度上改善Mesh网的服务质量。

文献“基于PSO的无线Mesh网关优化部署算法[J].传感技术学报，2008”，提出了一种基于粒子群算法进行求解来部署Mesh网关。该方法首先进行网络模型初始化，路由粒子编码信息，采用PSO迭代公式进行求解。但是该方法中采用固定的惯性权重，未区分社会因子。故该方法对粒子初始化速度和位置十分敏感，其本身不能有效的解决离散和组合优化等问题，而且参数的设定需要根据实际的情况进行设定，对动态网络网关部署适应度低，非常容易陷入局部最优解，导致收敛精度低甚至不收敛。

发明内容

为了克服现有技术的不足，本发明提供了一种基于自适应混合粒子群算法的Mesh网关部署优化方法，提出利用改进的混合粒子群算法——自适应混合粒子群优化(Adaptive Hybrid Particle Swarm Optimization，AHPSO)算法，来解决全局粒子群算法(PSO)算法在动态网络的网关部署陷入局部最优解的问题。首先基于路由节点位置的具体分布，建立网关节点和邻近节点的拓扑关系，建立模型来计算其适值函数，然后采用改进惯性权重和社会因子AHPSO算法，对其寻找全局最优解，最后根据节点粒子部署历史记录各类最优位置，调整其速度，采用改进后的迭代函数进行迭代更新，求得最优解。本发明方法能够快速地收敛逼近于全局最优值，在较大的程度上能够防止陷入局部最优解，从而解决收敛精度低甚至不收敛的问题，同时提高了对动态网络网关部署的适应度。

本发明解决其技术问题所采用的技术方案包括如下步骤：

步骤1：初始化节点粒子的信息，部署m个网关节点，每个节点粒子有n维，第i个网关节点粒子的坐标表示为：Xi＝(xi1,xi2,xi3,…xin)，第i个网关节点粒子的速度表示为：Vi＝(vi1,vi2,vi3,…vin)，设置最大迭代次数num和收敛阈值ε；

步骤2：定义与网关wk的距离小于通信半径的节点组成的集合为网关邻接集合GASk；网络中的任一节点到网关wk的跳数表示为：

其中vi、vj分别表示第i个节点和第j个节点；

则适值函数f(X)表示为：

其中，S表示Mesh网的规模；

步骤3：使用适值函数f(X)更新个体最优解，即节点粒子在部署过程中的历史最优位置Pi＝(pi1,pi2,pi3,…pin)，接着更新全局最优解，即整个粒子群在飞行过程中的历史最优位置Pg＝(pg1,pg2,pg3,…pgn)，接着更新粒子的邻域的最优值

步骤4：更新迭代次数N，采用改进后的sigmoid函数确定惯性权重ω，表示如下：

式中：e为自然常数，K为sigmoid曲线最大值，ke为sigmoid曲线的曲率，即曲线的变化速率；

步骤5：将惯性权重ω带入第i个节点粒子的速度和位置更新迭代公式(4)和式(5)：

其中，Vit+1为t+1时刻的节点粒子的速度，Vit为t时刻的节点粒子的速度，为t+1时刻的节点粒子的位置，为t时刻的节点粒子的位置；C1为节点粒子的个体学习因子，其值为一个加速度常数；C2为节点粒子的社会学习因子，其值为一个加速度常数；ξ和η为0到1范围内的随机数；q为全局社会因子和局部社会因子相对所占的比重，0

步骤6：判定是否达到最大迭代次数num或者连续两次计算结果间的差值小于收敛阈值ε，满足其中任一条件时就结束迭代，否则重复步骤4和步骤5，反复迭代更新后，得到最优解。

优选地，所述最大迭代次数num取值在240～260之间，收敛阈值ε取值在0.0003～0.001之间。

本发明的有益效果如下：

与采用PSO算法进行网关部署相比较，AHPSO算法的整体优化效果要优于传统PSO算法,PSO算法受到网络结构本身的影响较小，但是受到随机化初始的初值影响较大，也相对容易陷入局部最优。AHPSO算法采用自适应权重和局部搜索后，在一定程度上有效关联了无线Mesh网络的拓扑结构，更新粒子的速度变化，增加的局部搜索使得算法的搜索精度高，不容易陷入局部最优解，而且稳定性强。

附图说明

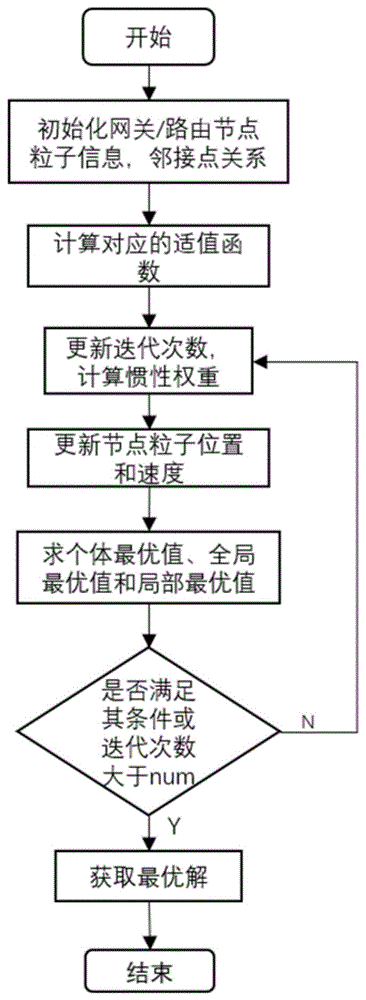
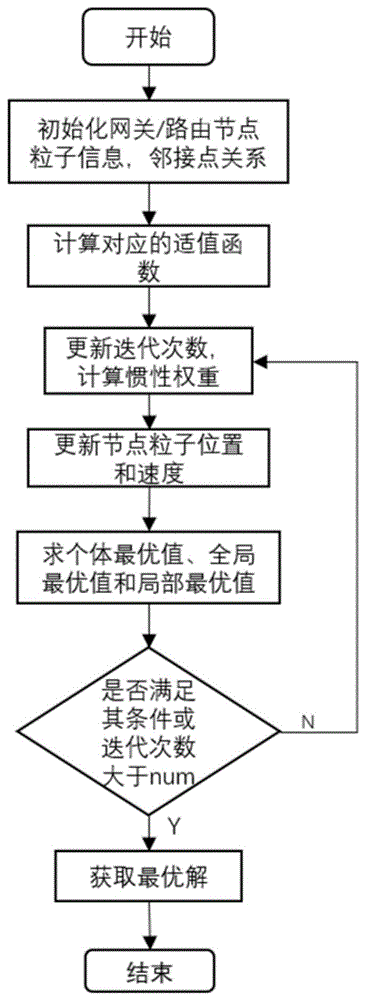
图1是本发明方法流程图。

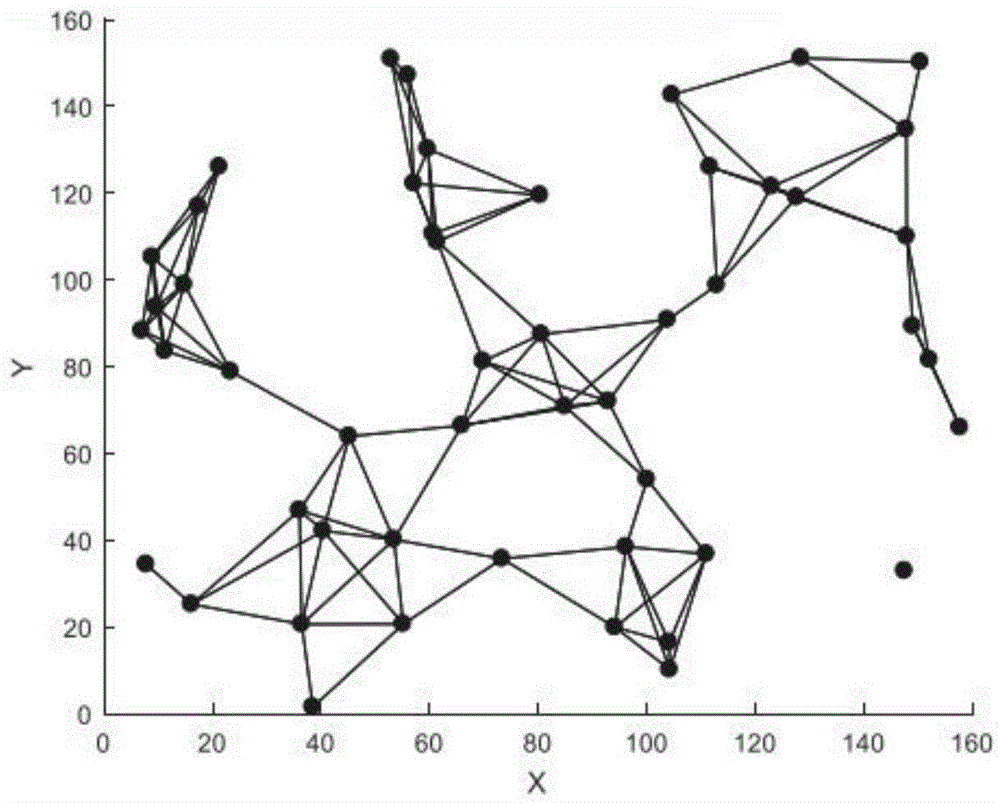
图2是本发明实施例根据实际场景路由节点位置画的部署分布图。

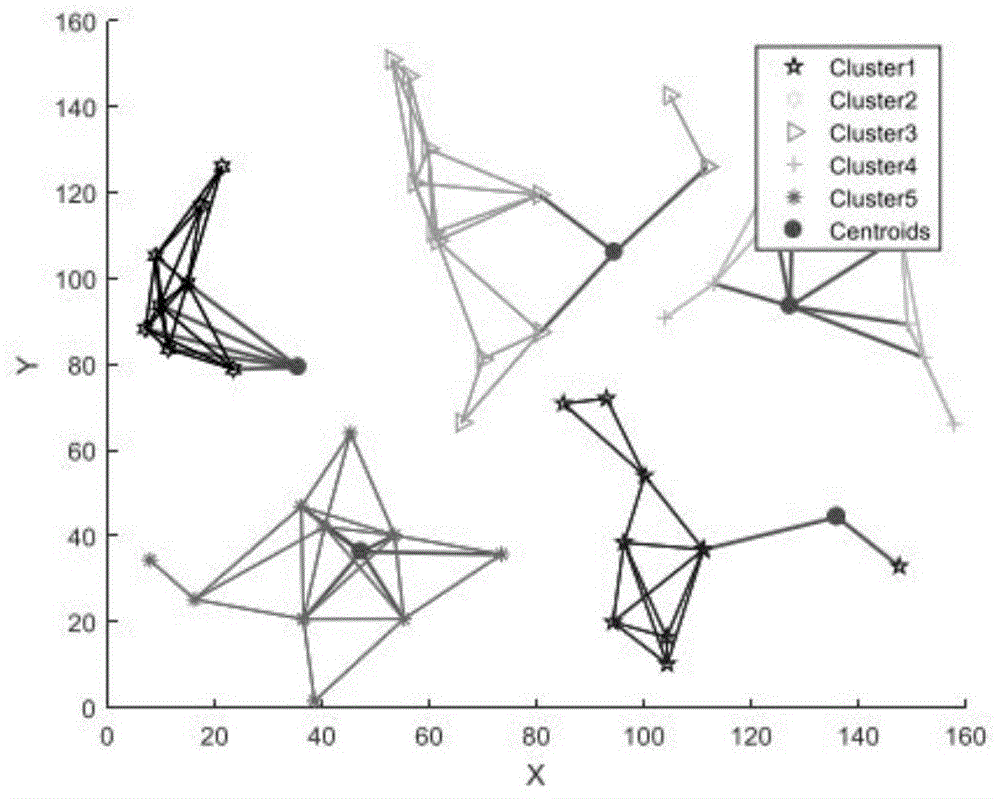
图3是本发明实施例网关路由节点的部署优化结果图。

具体实施方式

下面结合附图和实施例对本发明进一步说明。

一种基于自适应混合粒子群算法的Mesh网关部署优化方法，包括如下步骤：

步骤1：初始化节点粒子的信息，部署m个网关节点，每个节点粒子有n维，第i个网关节点粒子的坐标表示为：Xi＝(xi1,xi2,xi3,…xin)，第i个网关节点粒子的速度表示为：Vi＝(vi1,vi2,vi3,…vin)，设置最大迭代次数num和收敛阈值ε；

步骤2：定义与网关wk的距离小于通信半径的节点组成的集合为网关邻接集合GASk；网络中的任一节点到网关wk的跳数表示为：

则适值函数f(X)表示为：

步骤3：使用适值函数f(X)更新个体最优解，即节点粒子在部署过程中的历史最优位置Pi＝(pi1,pi2,pi3,…pin)，接着更新全局最优解，即整个粒子群在飞行过程中的历史最优位置Pg＝(pg1,pg2,pg3,…pgn)；

步骤4：更新迭代次数N，采用改进后的sigmoid函数确定惯性权重ω，表示如下：

式中：e为自然常数，K为sigmoid曲线最大值，ke为sigmoid曲线的曲率，即曲线的变化速率；

步骤5：将惯性权重ω带入第i个节点粒子的速度和位置更新迭代公式(4)和式(5)：

其中，Vit+1为t+1时刻的节点粒子的速度，Vit为t时刻的节点粒子的速度，为t+1时刻的节点粒子的位置，为t时刻的节点粒子的位置；C1为节点粒子的个体学习因子，其值为一个加速度常数；C2为节点粒子的社会学习因子，其值为一个加速度常数；ξ和η为0到1范围内的随机数；q为全局社会因子和局部社会因子相对所占的比重，0

步骤6：判定是否达到最大迭代次数num或者连续两次计算结果间的差值小于收敛阈值ε，满足其中任一条件时就结束迭代，否则重复步骤4和步骤5，反复迭代更新后，得到最优解。

优选地，所述最大迭代次数num取值在240～260之间，收敛阈值ε取值在0.0003～0.001之间。

具体实施例：

参照图1，首先采集Mesh网络多网关特征场景的节点分布位置，并处理得到节点的分布图，然后建立最小跳数的计算模型，即MESH网关部署的优化问题，转化为上述计算模型求最优解问题，采用改进后的混合粒子群算法进行求解，多次反复迭代，求得实际网关节点的部署最优方案。

1、由Mesh网络场景与传感器节点实际部署位置数据,建立路由节点地理位置分布图，根据路由节点通信范围计算得到路由节点与网关、传感器的连接参数，进而构建其拓扑连接图，计算得到mesh网络规模的大小S。

2、参照图2，初始化图中的50个节点分布图，每个节点粒子坐标Xi＝(xi1,xi2)，速度表示为：Vi＝(vi1,vi2)，同时设定迭代次数240次和迭代结果之差阈值0.0005。

3、以每个路由器通信距离为半径，路由器候选部署位置为每个中心点，得到候选部署位置无线链路连接参数，根据候选部署位置以及传感器节点位置，结合路由器与传感节点通信范围。整个网络的第k个网关wk的坐标wk＝(ak,bk)，与网关wk的距离小于通信半径的节点组成的集合称为网关邻接集合GASk(Gateway adjacency set)，那么网络中的任一节点到网关的跳数大小写成下式：

计算得到适值函数：

4、计算适值函数后，根据适值函数f(X)的结果来更新节点最优解，即该节点在部署过程中的历史最优位置Pi＝(pi1,pi2)，接着更新全局最优解，即整个网关节点在飞行过程中的历史最优位置Pg＝(pg1,pg2)。

5、更新迭代次数，采用改进后的sigmoid函数来计算迭代公式的惯性权重：

6、将惯性权重ω带入到迭代公式，第i个节点粒子的速度和位置更新公式分别如下：

式中：

ω为惯性因子，其值为非负数。当ω较大时，全局的搜索能力强，局部的搜索能力弱，当ω较小时，全局的搜索能力弱，局部的搜索能力强。

C1为粒子的个体学习因子，其值为一个加速度常数。

C2为粒子的社会学习因子，其值亦为一个加速度常数。

ξ和η为一个0到1范围内的随机数，可避免粒子过早收敛，增加粒子群广域搜索能力。

q为全局社会因子和局部社会因子相对所占的比重，0

7、判断是否符合迭代次数和阈值设置，如果未到达全局最优解，迭代次数加1，重复第5、6、7步，通过反复迭代更新计算，得到最优部署方案，如图3所示。