1.一种基于基于幂均算子和DS证据理论实现故障诊断的方法。其特征在于包括下述步骤:步骤一:确定辨识框架的方法为:考虑到设备的N种故障模式可以构造如下识别框架:θ={X0,X1,X2,...,Xn},其中,X0代表没有故障发生,X1,X2,...,Xn代表该故障的存在,我们可以构造X的幂集如下:2X={φ,{X0},{X1}...,{XN},{X0,X1},,...,{X0,...,Xi},...,{X0,...,XN}},多元素子集表示不确定多个命题中的哪个命题发生例如,{X0,X1}被视为一个不确定的状态,它不确定发动机是处于无故障状态X0还是故障模式X1;Xj是一个描述第j种故障(引擎状态)的特征向量Xj=[xj1 xj2 …xjn],xji是第j种故障的第i种特征,i=1,2,...,n,j=1,2,...,n;这个矩阵可以看作是故障原型的表示;用Sk表示从第k种传感器获得的测量向量:Ski表示Sk的第i个元素,i=1,2,...,mk,其中mk是第k个传感器获得的元素个数,∑mk=n,用S表示所有传感器的测量值,则S=[S1 S2 ... Sk]=[s1 s2 ... sn];对于{X0},{X1}...,{XN},即H1,...,HN+1,N+1个特征向量可以由样本量测得,它们也是辨识框架的幂集中单子集的特征向量,由于多子集表示根据所给出的数据无法确定发动机的状态,所以这里我们通过多子集各元素的平均特征值来构造多子集的特征值,例如,{HN+2}的特征向量为:HN+2={X0,X1}=[h(N+2)1,h(N+2)2,...,h(N+2)n],其中步骤二:获取样本数据的特征矩阵为:获取当待测设备处于无故障模式和各个故障模式时,传感器多次测量所得的数据,使用幂均算子得到特征值,公式为其中Sup(ai,aj)表示aj对ai的支持度,T(ai)表示除了ai本身,其他所有值对ai的支持度,持度函数为通过上述公式可得特征值矩阵,步骤三:生成基本概率分配函数:根据测量得到设备的数据,与特征值进行相似度对比,得到基本概率分配,直观来说,就某k传感器而言,Sk与Xj越相似,发生第j个故障的可能性越大,相对地,Sk与Xj相似度越低,第j个故障的可能性越小,使用Minkowski距离来度量测量特征值和故障原型之间的距离,Minkowski距离定义如下:dkj表示Sk与Xj的距离,α为一个恒定的常参数,所有传感器测量值与所有故障原型之间的距离可以以矩阵形式表示为:矩阵D中的每一行表示从一个传感器获得的测量值与所有故障原型之间的距离;D的每一列是一个故障原型到所有传感器测量值的距离,根据从第k个传感器获得的信息,距离dkj越小,第j个故障就越有可能发生,将pkj定义为:归一化后以矩阵形式表示,我们可以得到基本概率分配矩阵:其中pk=[pk1 pk2 ... pkN],k=1,2,...,M;每一行pk可以看作是第k个传感器得到的对于故障集合的基本概率分配函数(N个故障),并且对P矩阵按照传感器的不同分为多组BPA;步骤四:证据融合对多组BPA,使用D-S证据理论进行信息融合,D-S证据理论融合规则为:对于辨识框架θ下的一组概率分配函数m1,m2,...,mn而言,该融合公式为:步骤五:决策分析证据融合后,将多子集均分给单子集,为最终融合结果,其具体数值既为融合结果。
技术领域
本发明涉及故障诊断领域,是一种基于幂均算子和DS证据理论实现故障诊断的方法。
背景技术
故障诊断技术是一门紧密结合生产实际的工程科学,是现代化生产发展的产物。随着现代科学技术在设备上的应用,设备的结构越来越复杂,功能也越来越完善,自动化程度越来越高,由于许多无法避免的因素影响,会导致设备出现各种故障,从而降低或失去预定的功能,甚至会造成严重的乃至灾难性的事故。
故障诊断技术就是在设备运行中或基本不拆卸设备的情况下,掌握设备的运行状况,根据对被诊断对象测试所取得的有用信息进行分析处理,判断被诊断对象的状态是否处于异常状态或故障状态。
信息融合技术是协同利用多源信息,以获得对事物或目标更客观、更本质认识的信息综合处理技术,是智能科学研究的关键技术之一。在诸多的融合模型和方法中,D-S证据理论算法是最为有效的算法之一。证据理论把概率论中的基本事件空间拓宽为基本事件的幂集,又称为辨识框架,在辨识框架上建立了基本概率分配函数(Basic ProbabilityAssignment,BPA)。此外,证据理论还提供了一个Dempster组合规则,该规则可以在没有先验信息的情况下实现证据的融合。特别地,当BPA只在辨识框架的单子集命题上进行分配时,BPA就转换为概率论中的概率,而组合规则的融合结果与概率论中的Bayes公式相同。从这个角度来看,DS证据理论能够比概率论更有效地表示和处理不确定信息,这些特点使其在信息融合领域得到了广泛的应用。正是由于DS证据理论在不确定知识表示方面具有优良的性能,所以近几年其理论和应用发展较快,该理论在多传感器信息融合、医学诊断、军事指挥、目标识别方面发挥了重要作用。
证据理论有诸多优点,将其应用在故障诊断中可以较好的处理出现在设备传感器信号中的不确定信息。
发明内容
为了实现故障诊断,本发明基于DS证据理论,提供一种故障诊断的方法。使用该方法实现的故障诊断能够较好的处理设备传感器信号中的不确定信息,准确地对设备做出故障诊断。
本发明解决其技术问题所采用的技术方案包括如下步骤:
步骤一:确定辨识框架的方法为:
考虑到设备的N种故障模式可以构造如下识别框架:θ={X0,X1,X2,...,Xn},其中,X0代表没有故障发生,X1,X2,...,Xn代表该故障的存在,我们可以构造X的幂集如下:2X={φ,{X0},{X1}...,{XN},{X0,X1},,...,{X0,...,Xi},...,{X0,...,XN}},多元素子集表示不确定多个命题中的哪个命题发生例如,{X0,X1}被视为一个不确定的状态,它不确定发动机是处于无故障状态X0还是故障模式X1;Xj是一个描述第j种故障(引擎状态)的特征向量Xj=[xj1 xj2 ... xjn],xji是第j种故障的第i种特征,i=1,2,...,n,j=1,2,...,n;这个矩阵可以看作是故障原型的表示;用Sk表示从第k种传感器获得的测量向量:k=1,2,...,M,Ski表示Sk的第i个元素,i=1,2,...,mk,其中mk是第k个传感器获得的元素个数,∑mk=n,用S表示所有传感器的测量值,则S=[S1 S2 ... Sk]=[s1 s2 ... sn];对于{X0},{X1}...,{XN},即H1,...,HN+1,N+1个特征向量可以由样本量测得,它们也是辨识框架的幂集中单子集的特征向量,由于多子集表示根据所给出的数据无法确定发动机的状态,所以这里我们通过多子集各元素的平均特征值来构造多子集的特征值,例如,{HN+2}的特征向量为:HN+2={X0,X1}=[h(N+2)1,h(N+2)2,...,h(N+2)n],其中
步骤二:获取样本数据的特征矩阵为:
获取当待测设备处于无故障模式和各个故障模式时,传感器多次测量所得的数据,使用幂均算子得到特征值,公式为其中Sup(ai,aj)表示aj对ai的支持度,T(ai)表示除了ai本身,其他所有值对ai的支持度,持度函数为通过上述公式可得特征值矩阵,
步骤三:生成基本概率分配函数:
根据测量得到设备的数据,与特征值进行相似度对比,得到基本概率分配,直观来说,就某k传感器而言,Sk与Xj越相似,发生第j个故障的可能性越大,相对地,Sk与Xj相似度越低,第j个故障的可能性越小,使用Minkowski距离来度量测量特征值和故障原型之间的距离,Minkowski距离定义如下:
k=1,2,...M;j=1,2,...N,dkj表示Sk与Xj的距离,α为一个恒定的常参数,所有传感器测量值与所有故障原型之间的距离可以以矩阵形式表示为:
矩阵D中的每一行表示从一个传感器获得的测量值与所有故障原型之间的距离;D的每一列是一个故障原型到所有传感器测量值的距离,根据从第k个传感器获得的信息,距离dkj越小,第j个故障就越有可能发生;将pkj定义为:归一化后以矩阵形式表示,我们可以得到基本概率分配矩阵:
其中pk=[pk1 pk2 ... pkN],k=1,2,...,M;每一行pk可以看作是第k个传感器得到的对于故障集合的基本概率分配函数(N个故障),并且对P矩阵按照传感器的不同分为多组BPA;
步骤四:证据融合
对多组BPA,使用D-S证据理论进行信息融合,D-S证据理论融合规则为:对于辨识框架θ下的一组概率分配函数m1,m2,...,mn而言,该融合公式为:
步骤五:决策分析
证据融合后,将多子集均分给单子集,为最终融合结果,其具体数值既为融合结果。
本发明的有益效果在于本发明采用幂均算子与多子集的证据距离相结合实现故障诊断,具有计算简单的优点;本发明用幂均算子构建特征值,解决了较大测量误差的样本点对构建特征值的影响;本发明提出的基于证据距离的基本概率分配函数生成方法,很好的实现了对模糊信息的处理;本发明提出的故障诊断方法,可以实现对设备的故障诊断。
附图说明
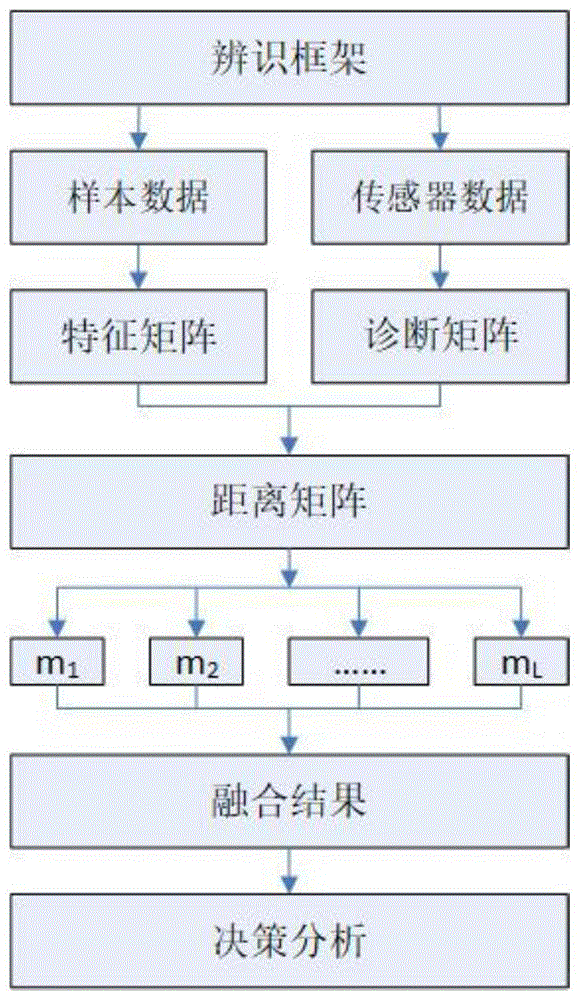
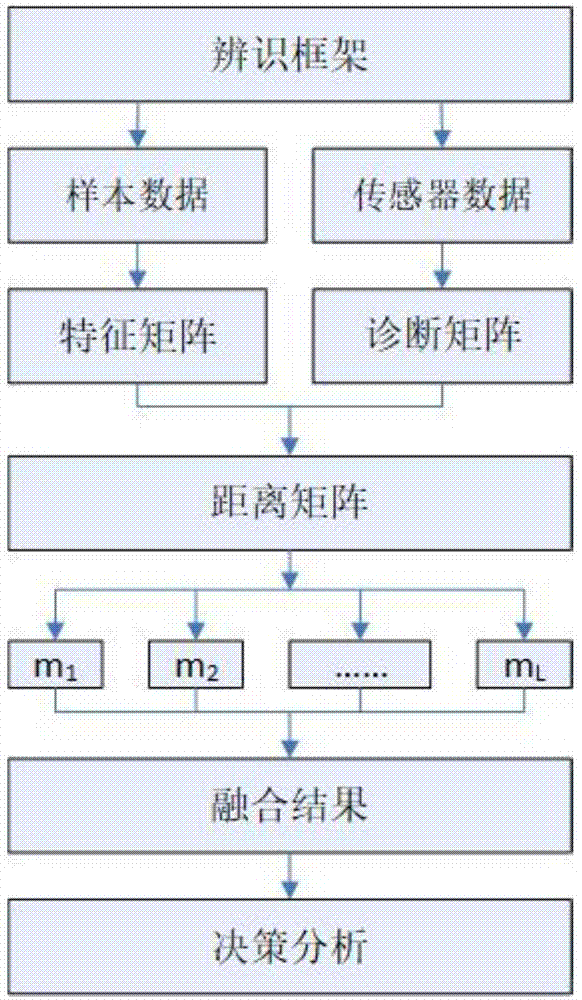
图1本发明实现的总流程图。
图2是无故障时特征值样本数据。
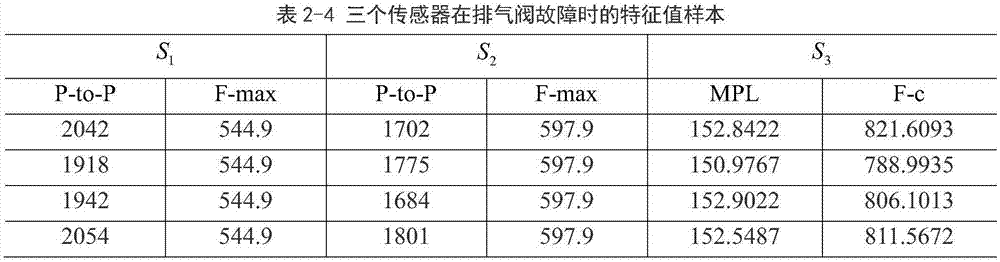
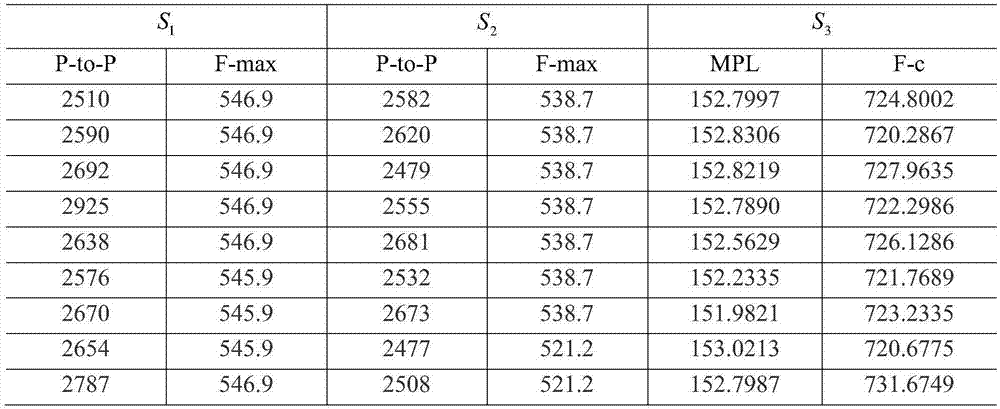
图3是排气阀故障时的特征值样本数据。
图4是活塞环故障时的特征值样本。
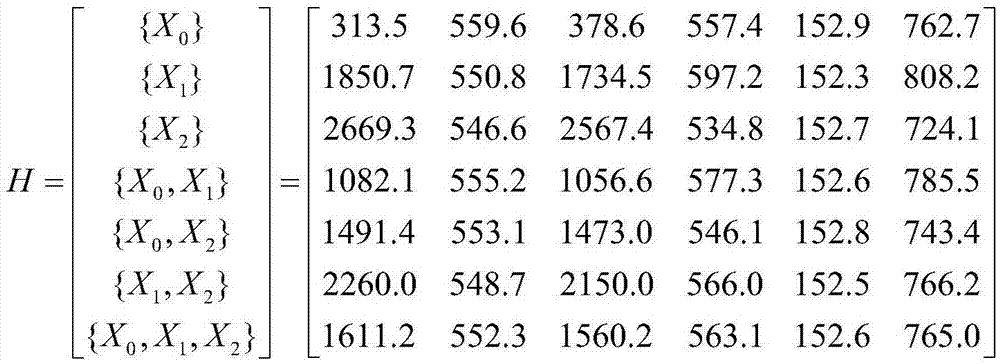
图5是发动机特征值矩阵。
图6是基本概率分配矩阵。
图7是BPA矩阵。
图8是融合结果矩阵
具体实施方式
下面结合附图和实例对本发明进一步说明。此处给出发动机故障诊断的实例,实验数据如图2、图3和图4。发动机的三种状态:“无故障:X0”,“排气阀故障:X1”和“活塞环故障:X2”。使用三个传感器采集数据:一个加速度传感器和一个声学传感器。一个加速度传感器安装在靠近出气阀的气缸盖上,标记为S1;另一个加速度传感器安装在进气阀附近的气缸盖上,标记为S2;声学传感器位于气缸盖正上方,标记为S3。对于加速度信号,我们计算它们在时域中的峰峰值(P-to-P)和最大频谱的频率(F-max)。对于声信号,我们计算平均压力水平(MPL)和频谱的中心频率(F-c)。
步骤一:确定辨识框架的方法为:
当考虑到发动机的两种可能故障模式,发动机共有三种状态:发动机无故障X0、排气阀故障X1和活塞环故障X2,此时,辨识框架构建如下:X={X0,X1,X2},X的幂集为:
2X={φ,{X0},{X1},{X2},{X0,X1},{X0,X2},{X1,X2},{X0,X1,X2}};
步骤二:获取样本数据的特征矩阵为:
获取当待测设备处于无故障模式和各个故障模式时,传感器多次测量所得的数据,使用幂均算子得到特征值,公式为其中Sup(ai,aj)表示aj对ai的支持度,T(ai)表示除了ai本身,其他所有值对ai的支持度,持度函数为且K=1,α=1,通过上述公式可得特征值矩阵,如图5;
步骤三:生成基本概率分配函数:
根据测量得到设备的数据,与特征值进行相似度对比,得到基本概率分配,直观来说,就某k传感器而言,Sk与Xj越相似,发生第j个故障的可能性越大,相对地,Sk与Xj相似度越低,第j个故障的可能性越小,使用Minkowski距离来度量测量特征值和故障原型之间的距离,Minkowski距离定义如下:
k=1,2,...M;j=1,2,...N,dkj表示Sk与Xj的距离,α为一个恒定的常参数,所有传感器测量值与所有故障原型之间的距离可以以矩阵形式表示为:
矩阵D中的每一行表示从一个传感器获得的测量值与所有故障原型之间的距离;D的每一列是一个故障原型到所有传感器测量值的距离,根据从第k个传感器获得的信息,距离dkj越小,第j个故障就越有可能发生,将pkj定义为:归一化后以矩阵形式表示,我们可以得到基本概率分配矩阵:
其中pk=[pk1 pk2 ... pkN],k=1,2,...,M;每一行pk可以看作是第k个传感器得到的对于故障集合的基本概率分配函数(N个故障),并且对P矩阵按照传感器的不同分为多组BPA;对于一待诊断发动机,通过三个传感器测得的特征值为S1=[2117.6548.8],S2=[2031.6570.1],S3=[152.3765.5],传感器的测量值可以表示为S=[S1 S2 S3]=[2117.6 548.8 2031.6 570.1 152.3 765.5],采用欧氏距离(α=2)得到距离矩阵后,可得到基本概率分配矩阵如图6,既由三个传感器所得三组BPA如图7;
步骤四:证据融合:
对图7的三组BPA,使用D-S证据理论进行信息融合,D-S证据理论融合规则为:对于辨识框架θ下的一组概率分配函数m1,m2,...,mn而言,该融合公式为:
融合结果如图8;
步骤五:决策分析
将图8数据中多子集均分给单子集,得到最终融合结果,得到融合结果m':m'({X0})=0.2376,m'({X1})=0.5969,m'({X2})=0.1655,由结果可知,排气阀故障概率最大。



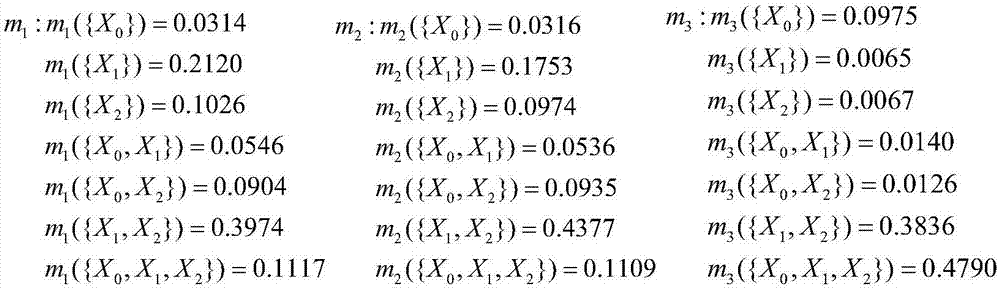
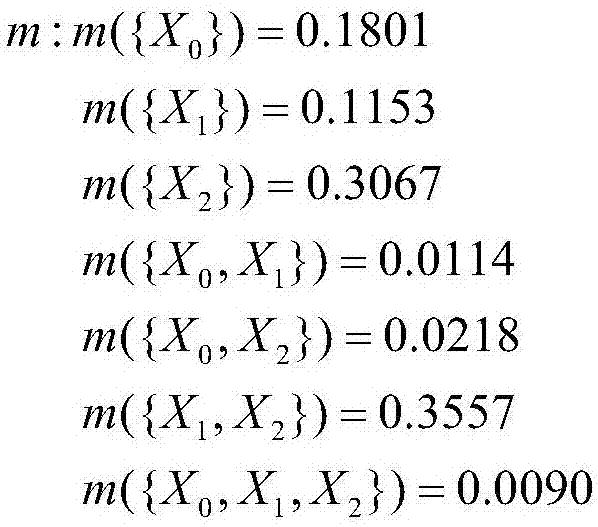


评论
全部评论
共{{commentCount}}条{{rs.Msg_Content}}