技术领域

本发明属于多能源电力系统的优化调度技术领域，具体涉及基于鹦鹉算法的多能源电力系统优化调度的方法。

背景技术

随着工业的快速发展，传统的化石能源也在快速的消耗，能源危机成了迫在眉睫的问题。为了解决能源危机问题,只有传统的一种供能方式是不够的，人们开始对电能、气能、热能等多种形式的能源进行综合利用研究。过去的能源系统中，电网、气网、热网等不同的能源网络是相互独立运行的，互联程度不高，不利于提高能源的综合利用率，也不利于多个能源系统的优化运行，而近些年发展的多能源系统能够打破这个壁垒，因此多能源电力系统的优化调度也十分重要。

多能源电力系统孤岛运行模式下优化调度策略流程图过于繁杂，对比其他多种算法，粒子群算法(Particle Swarm Optimization,PSO)有容易理解，所需控制参数不多，容易得到期望结果，有一些的并行性等特点。但PSO具有容易陷入局部最优和低精度这两大缺点，国内外学者近几年致力于改进这一算法，但是结果却都不尽人意，蝙蝠算法在PSO基础上采用频率调谐的新型算法，虽然在收敛方面有所改观，但寻优精度大幅下降。在应对井喷式增长的能量负荷计算的需求下，果蝇分析算法虽然在优化时具有较高精度，但是比传统的粒子群优化算法更容易陷入与功率相关的局部最优这一情况。从这些例子可以看出近些年PSO的改进陷入了要想增加优化规模、提高算法寻优效率和精度，就无法彻底解决PSO缺陷，要想彻底解决PSO缺陷，就无法增加优化规模、提高算法寻优效率和精度的怪圈。

发明内容

为突破上述难题，本发明提出了一种基于鹦鹉算法的多能源电力系统优化调度的方法，分别解决传统粒子群算法容易陷入局部最优和低精度的问题，具有高效，准确的优点。

本发明所采用的技术方案是，基于鹦鹉算法的多能源电力系统优化调度的方法，其特征在于，包括以下步骤：

步骤1，建立考虑经济性和环保性的多能源电力系统优化调度的数学模型；

步骤2，设计鹦鹉算法；

步骤3，构建三种不同的多能源电力系统优化调度策略，对鹦鹉算法的有效性进行验证。

所述的步骤1，建立考虑经济性和环保性的多能源电力系统优化调度的数学模型,具体步骤为：

步骤1.1，得到包含光伏发电、风力发电机、微型燃气轮机、燃料电池、储能单元的多能源电力系统各个发电单元的输出特性和成本组成：

1)光伏发电单元(Photovoltaic cell,PV)：

光电的主要特性如下所示：

式中，Kr＝0.0017(A/℃)，Tr＝301.18K，其中P是光伏板发出的功率，V是光伏板发出的电压，I是光伏板发出的电流，m是并联板电池数，Iph是光伏组件经由光照射所产生，I0是初始电流，q是电池内部电子电量常量，Rs是串联单向电阻，n是串联电池数，A是二极管特性拟合系数，Kr是玻尔兹曼常数，Tr是标准温度，T是测量时刻的温度；

在实际应用时，由于系统出力受光伏电池环境温度和太阳辐射下系统强度的多种因素影响，所以用标准条件下来修正：

式中：GSTC＝1000W/m2，k＝-0.47％/℃，Tr＝25℃，GSTC是标准太阳辐照强度，GING是实际太阳辐照强度，k是功率温度系数，Tc是实际温度，Tr是标准温度；

太阳能光伏燃料电池直接从太阳获取的能量，属于可再生能源，还应该全方位考量其工作费用和维修费用；

2)风力发电单元(Wind Turbine generator,WT)：

风电的功率特性如下：

在实际条件下，此处不考虑环保成本与利用率成本，只考虑其修理的成本，其中V是风机输入的风速，Vr是标准风速，Pr是标准功率，PWT是风机输出功率，Vco是风机切出风速，Vci是风机切入风速；

3)微型燃气轮机(Micro gas Turbine,MT)：

微型燃气轮机功率函数模型如下：

其中，ηMT是型通用燃气轮机的效率，PMT是型通用燃气轮机的输出功率；

微型通用燃气轮机的正常维护运行以及日常维护费用成本相关函数：

式中，KOMMT直接取0.047元/kWh，其中，KOMMT是微型通用燃气轮机的正常维护运行以及日常维护费用成本系数，COMMT是微型通用燃气轮机的正常维护运行以及日常维护费用成本；

微型燃汽轮机的外部污染治理排放系数及其治理费用和成本的函数计算如下式所示：

其中，CEMMT是微型燃汽轮机的外部污染治理排放系数及其治理费用和成本，λk是排放因子，αk是折扣系数；

4)燃料电池(Fuel Cell,FC)：

P为40kW，其功率输出PFC与发电效率ηFC的关系可由下式表示：

ηFC＝-0.0023PFC+0.6735 (7)

其中，ηFC是燃料电池的效率；

在维持燃料电池发电动力系统正常稳态持续发电的过程中，燃料电池的有效输入量和燃料电池输出能耗投入的发电成本的比例关系用下式进行表示：

式中：LHVng是天然气低热值取9.7kWh/m3，Cng是天然气成本，PFC(t)是t时刻燃料电池的功率，CFFC(t)是t时刻燃料电池费用，ηFC(t)是燃料电池效率；

燃料转化电池的正常工作运行以及维护管理成本可用下式来表示：

其中，CEMFC是燃料转化电池的正常工作运行以及维护管理成本，αk是折扣系数，λk是排放因子；

5)储能单元(BatteryTurbine,BT)：

充分考虑了多能源电力蓄电池的两种重要约束，即蓄电池充放电功率约束和蓄电池最大容量约束，所以便于蓄电池的应用在t时刻荷电状态(State Of Charge,SOC)可表示为：

式中，I是蓄电池的电流，PBT是蓄电池的功率，UBT是蓄电池的电压，SOC是蓄电池的荷电状态，σsdr是蓄电池的自放电率，ηbce是蓄电池的充放电效率，C是蓄电池的电池容量，Δt是时间间隔，取Δt＝1h,ηbce放电时其值为1，充电时一般在0.65～0.85范围内；

步骤1.2，构建多能源电力系统环保经济运行的目标函数：

1)经济成本目标函数

这一目标函数是使每个单元都有最小的操作成本，包括微电网与主网交互成本、运行维护成本、制热收益、孤网负荷补偿成本、制冷收益以及微电源的燃料成本，表示公式如下：

式中，C1是运行成本，Cf是燃料成本，COM是检修维护成本，Cgeid是微网主网交互成本，Csh是制热成本，Csc是制冷成本，CL是补偿成本，e、b是费用考虑系数，当这两个值取e＝1,b＝0时，系统并网工作，主网与系统之间存在交互成本；e＝0,b＝1，即系统孤网工作，要取掉一定比例的负荷，那么这种情况下就有切负荷补偿成本，

其中：

Cgrid(t)＝Cg(t)Pg(t)-Cs(t)Ps(t) (15)

Csh(t)＝Qho×Kho (16)

Csc(t)＝Qco×Kco (17)

CL(t)＝Cbu×PCL(t) (18)

其中，LHVng是天然气低热值取9.7kWh/m3，Cng是天然气成本，PFC(t)是t时刻燃料电池的功率，CFFC(t)是t时刻燃料电池费用，ηFC(t)是燃料电池效率；Pi是第i个发电单元的输出功率，ηi第i个发电单元的效率，COM是检修维护成本，KOMi是第i个发电单元正常维护运行以及日常维护费用成本系数，Cgrid是微网主网交互成本，Cg是微网向主网购电成本，Pg是微网向主网购电功率，Cs是微网向主网卖电成本，Ps是微网向主网卖电功率，Csh是制热成本，Qho是热值量，Kho是制热系数，Csc是制冷成本，Qco是冷值量，Kco制冷系数，CL是补偿成本，Cbu是微网支付的停电电量损失，PCL切负荷功率，n是发电单元总数，i是发电单元编号；

2)环保目标函数

这一目标函数是考虑到多能源电力系统的环境效益最大，即能源的污染排放和治理的成本最小，表示公式如下：

式中：C2是环保成本，CK处理污染物惩罚系数，rik第k类型排放的i个发电单元的输出功率系数，Pi是第i个发电单元的输出功率，α是外部折扣系数，rgridk是第k类型排放的微网主网交互系数，Cg是微网向主网购电成本，P是微网向主网购电功率，t是调度的时间，T是调度的总时间，M是排放类型(NOX、SO2或者CO2)数，k是排放类型，n是发电单元总数，i是发电单元编号；

步骤1.3，构建多能源电力系统环保经济运行的约束条件：

1)电功率平衡约束

其中，Pi是第i个发电单元发出的功率，Pball是蓄电池释放的功率，Pgrid是微网主网交互功率，PL是孤网下切负荷功率，β是运行系数，PCL是切负荷功率，当系统并网运行时，β＝0；当系统孤网运行时，β＝1；

2)冷热平衡约束

其中，Qho是制热量，是第k个冷热电联供系统制热量，Qco是制冷量，是第k个冷热电联供系统制冷量，是冷热电联供系统制热量最大值，是冷热电联供系统制热量最小值，是冷热电联供系统制冷量最大值，是冷热电联供系统制冷量最小值；M是冷热电联供系统的总数；

3)微源功率的限定值的约束

其中，和分别表示发电单元发出功率的最大值和最小值；

4)蓄电池运行约束

其中，Sin为输入荷电状态，SOCmin为最小荷电状态，SOCmax为最大荷电状态，Pball为蓄电池的充放电功率，为蓄电池最小的充放电功率，为蓄电池最大的充放电功率；

5)多能源电力系统与主网允许传输功率约束

其中，和分别表示电网传输功率的最大值和最小值。

所述的步骤2，设计鹦鹉算法，具体的步骤为：

步骤2.1，引入自适应权重法：

受到鹦鹉具有自我学习能力与不同环境适应能力的启发，引入自适应权重法；惯性运动权重w的线性速度公式描述了鹦鹉个体以非线性运动法作为计算物体惯性运动权重w的基本方法和应用策略，其改进的计算公式如下：

式中：wmax、wmin分别表示为最大权重值和最小权重值，一般取wmin＝4.0，wmax＝9.0；惯性权重和适应系数的最小值会随着自适应粒子的目标适应度函数值的大小改变而发生改变，所以该惯性权重又命名为自适应权重；

步骤2.2，引入学习因子：

在鹦鹉算法中，两异步速度变化的群算法学习因子c1、c2会随着优化时间的长短发生不同的改变，对鹦鹉个体优化加以下的要求：在鹦鹉个体的群算法开始和结束阶段，鹦鹉个体必须具有较大的自我参与学习的能力，应该需要加强其全局学习和搜索的能力；而在群算法寻优的快速开始和结束时，鹦鹉个体必须具有较弱的自我参与社会学习的能力和较强的自我社会学习的能力，因此可以加快鹦鹉种群算法收敛的速度，有利于快速的群算法收敛得到快速的全局最优解，具体的公式如下：

式中：c1是第1个学习因子，c1f是第1个最终学习因子，c1t是第1个初始学习因子，tmax是最大时间，t是时间，c2是第2个学习因子，c2f是第2个最终学习因子，c2t是第2个初始学习因子，取c1t＝c1f＝2.5，c1t＝c1f＝0.5。

所述的步骤3，构建三种不同的多能源电力系统优化调度策略，对鹦鹉算法的有效性进行验证，具体的步骤为：

步骤3.1，多能源电力系统的多目标函数处理方法：

1)多目标优化算法的通用模型：

式中：f(X)是总目标函数，f1(X),f2(X),…,fm(X)是m个不同的子目标函数，m表示个数的多少，gi(X)为不等式约束，i表示等式约束的个数，hj(X)表示等式约束，j表示等式约束的个数，X为n个变量x1,x2,…,xn所组成的n维决策变量，在多目标优化问题中，取不等式约束m≥2；等式约束取s.t.gi(X)≥0和hj(X)＝0；

2)多能源电力系统的多目标函数处理办法：

多目标优化的各个子目标较难同时实现总目标最优化，因此采用一种线性加权函数求和法对多目标进行了最优化，来实现多目标电力系统的优化，具体可以表示为：

minf(X)＝w1f1(X)+w2f2(X) (31)

式中：f(X)为总的目标函数，f1(X)为第1个目标函数，f2(X)为第2个目标函数，w1，w2分别表示第1个目标函数和第2个目标函数的权重。w1≥0,w2≥0，且满足w1+w2＝1，随机权重w1和w2由下式确定：

式中：ri是非负随机数，r1，r2是均是非负随机数；

步骤3.2，多能源电力系统的约束条件处理方法：

利用罚函数法处理约束条件，它将优化问题中含有不等式约束和等式约束的函数经过加权优化处理后，与原优化目标函数相结合，可以直接得到一个新的目标函数，此时，原约束问题转化成新的无约束条件的优化问题，对这个无约束的优化问题进行求解即可。

步骤3.3，构建三种不同的多能源电力系统优化调度策略：

根据多能源电力系统是否与主网之间的并网协同运行，确定微电源和主网的优先级，构建了以下管控策略：

策略一：微电源优先级高于主网，若微电源功率不够，则向主网购电；

策略二：微电源与主网优先级相同，若微电源电量不够，只能从主网购电；

策略三：微电源与主网优先级相同，若微电源电量不足，不限制从主网购电；

步骤3.4，采用鹦鹉算法求解三种不同的多能源电力系统优化调度策略：

采用鹦鹉算法对提出的三种不同的多能源电力系统优化调度策略进行求解；

首先，生成随机移动的鹦鹉种群，初始化全部随机鹦鹉个体的初始值和鹦鹉个体的移动时间v，并且随机设定鹦鹉个体移动位置以及各种随机粒子移动参数；

其次，评价每个鹦鹉个体的适应度，计算个体极值pbest及全局极值gbest，并根据相关公式对被测鹦鹉个体的移动区域和移动时间v的两个参数进行更新；

再次，对学习习惯性的权重因子进行调整，并通过比较迭代后鹦鹉个体的适应度值的大小与上一次迭代后鹦鹉个体的适应度值的大小，来决定是否要更新个体极值和全局极值；

最后，根据是否达到迭代的次数或者最大适应参数值没有发生变化两个条件来判断是否终止算法，若满足条件之一，则算法结束，若不满足，则重新进行初始化进行相关操作。

本发明的有益效果是：

使用的鹦鹉算法在传统粒子群算法的基础上增加自适应权重和学习因子，以此来改变传统粒子群算法容易陷入局部最优、低精度两大缺点。通过对相关案例进行求解和仿真，仿真的结果表明，对于不同目标函数、不同目标、不同运行策略下使用鹦鹉算法，都能快速、准确的求解该模型，证明了该算法的有效性。

附图说明

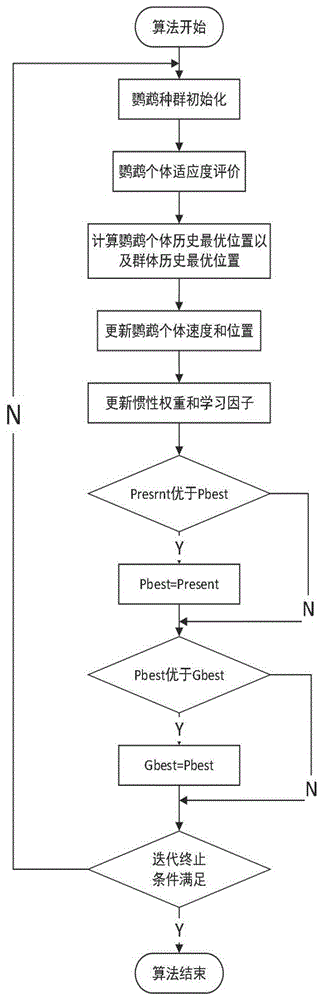
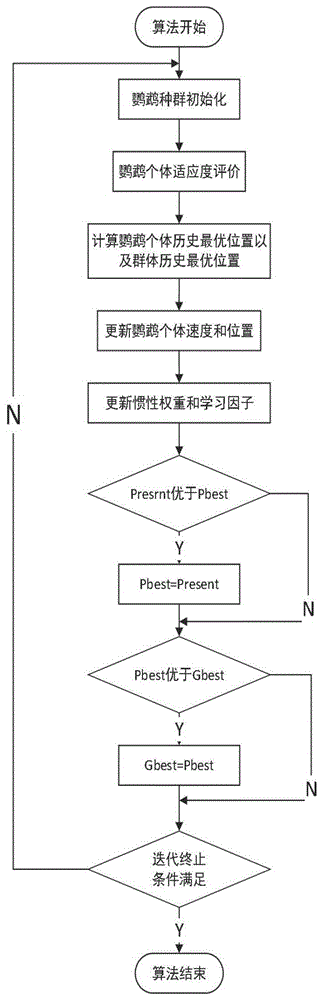
图1是基于鹦鹉算法的多能源电力系统优化调度数学模型的求解流程图。

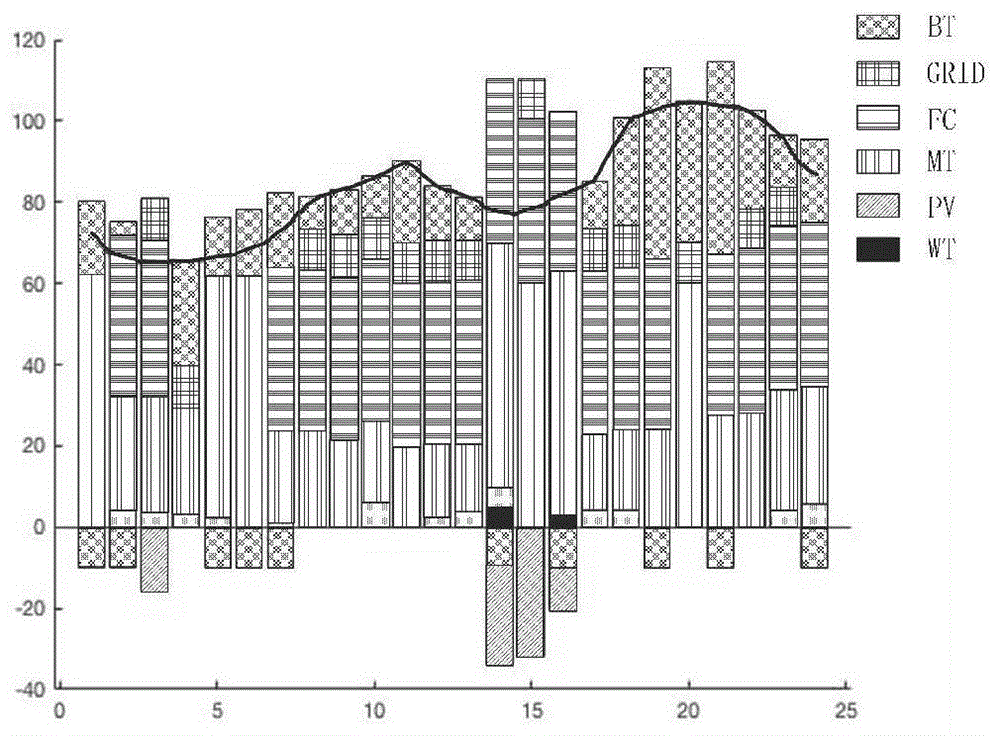
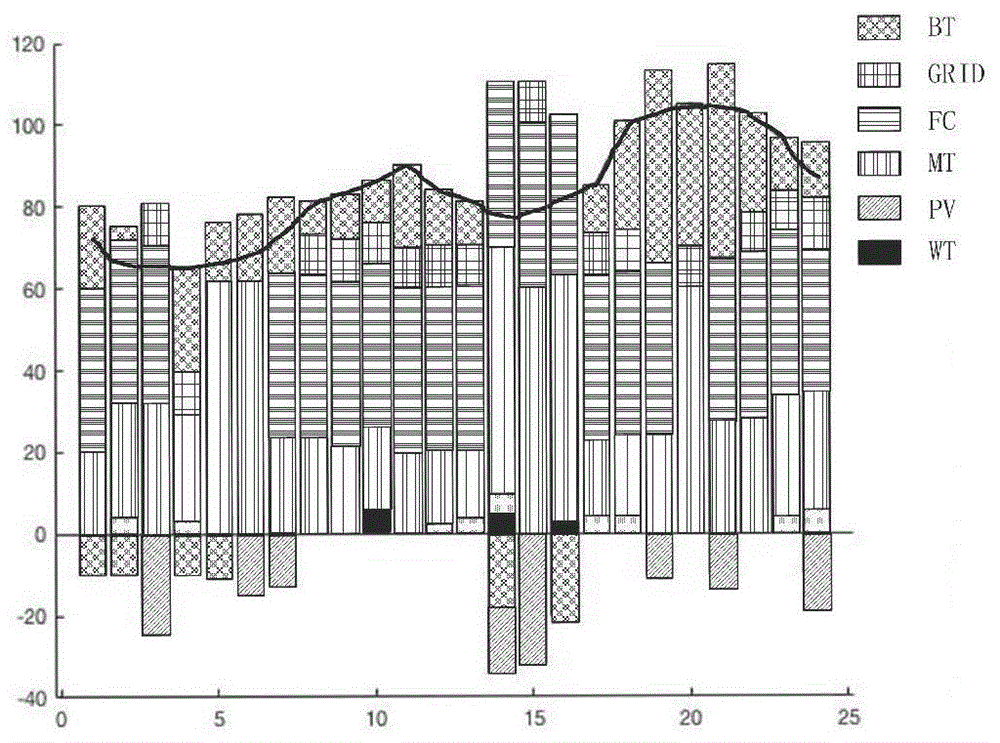
图2是采用策略三，即微电源与主网优先级相同，若微电源电量不足，不限制从主网购电，在冬季典型日目标权重系数w1＝w2＝0.5时的仿真结果分析图。

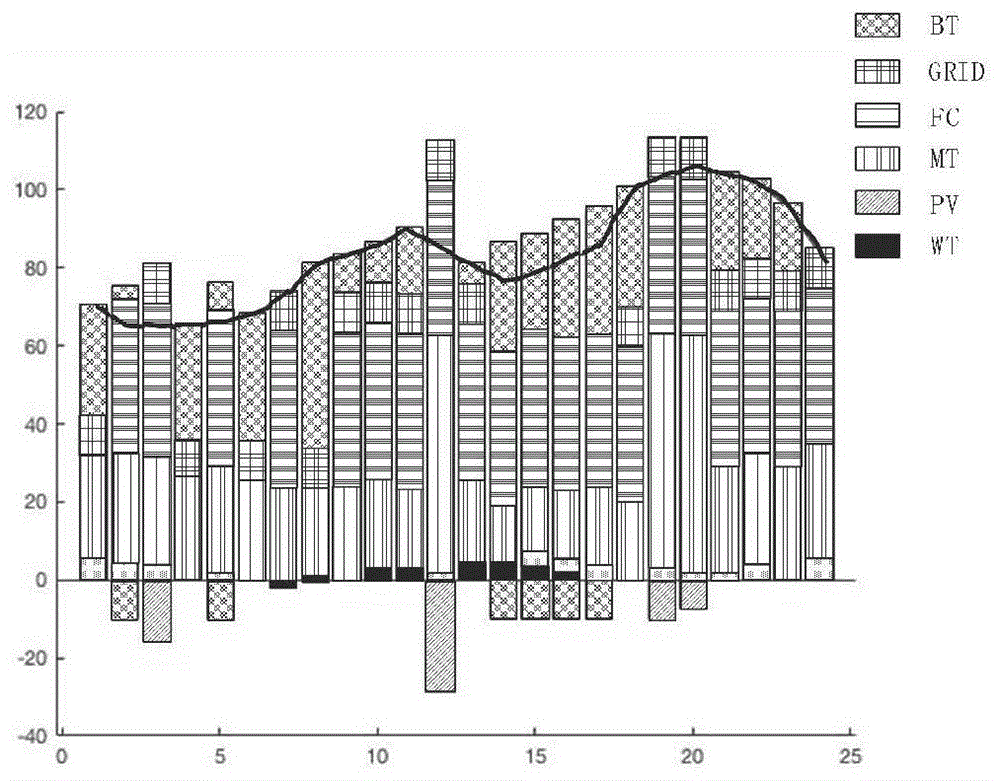
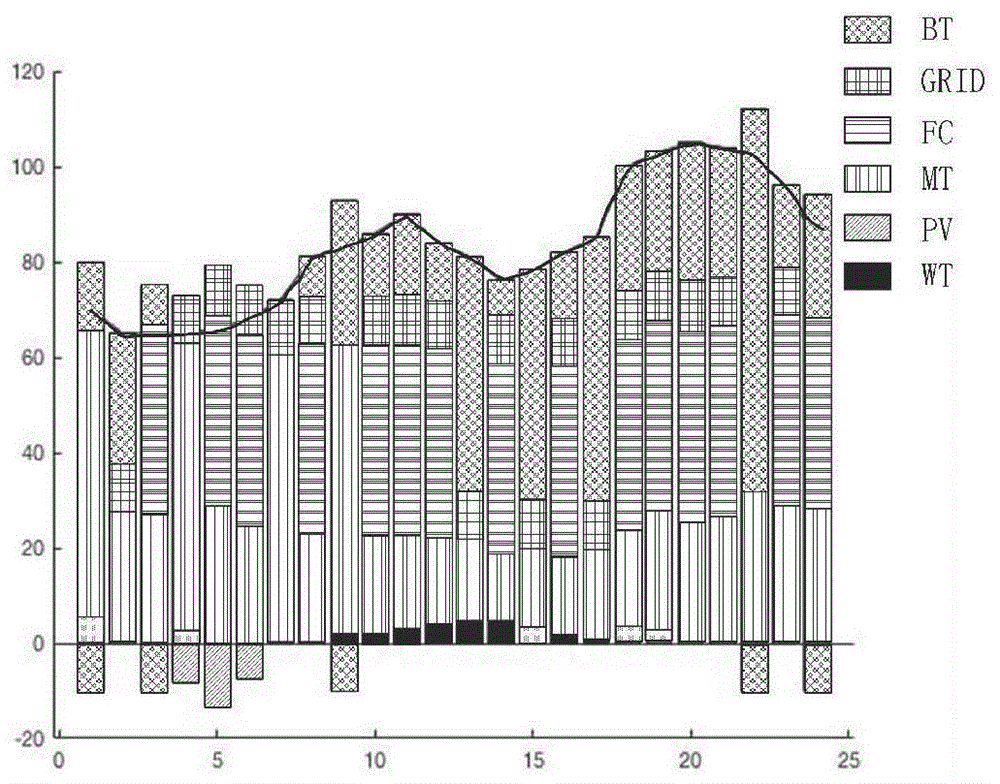
图3是采用策略三，在冬季典型日目标权重系数w1＝0.8,w2＝0.2时的仿真结果分析图。

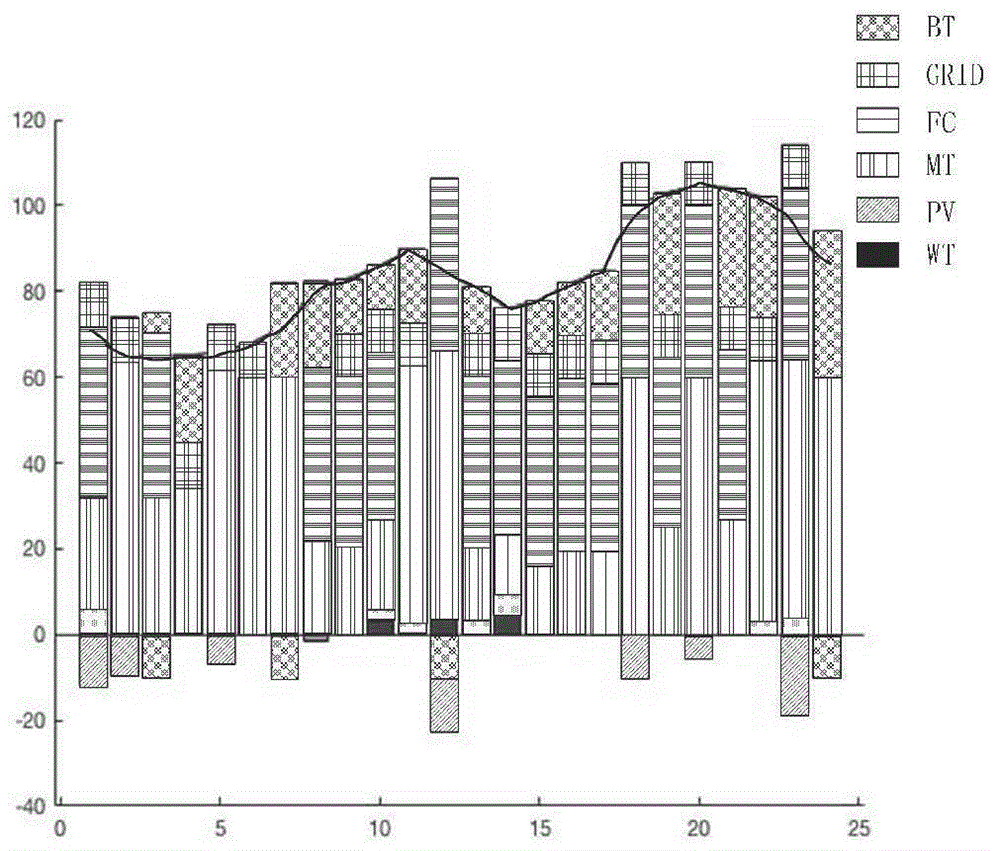
图4是采用策略三，在冬季典型日目标权重系数w1＝0.3,w2＝0.7时的仿真结果分析图。

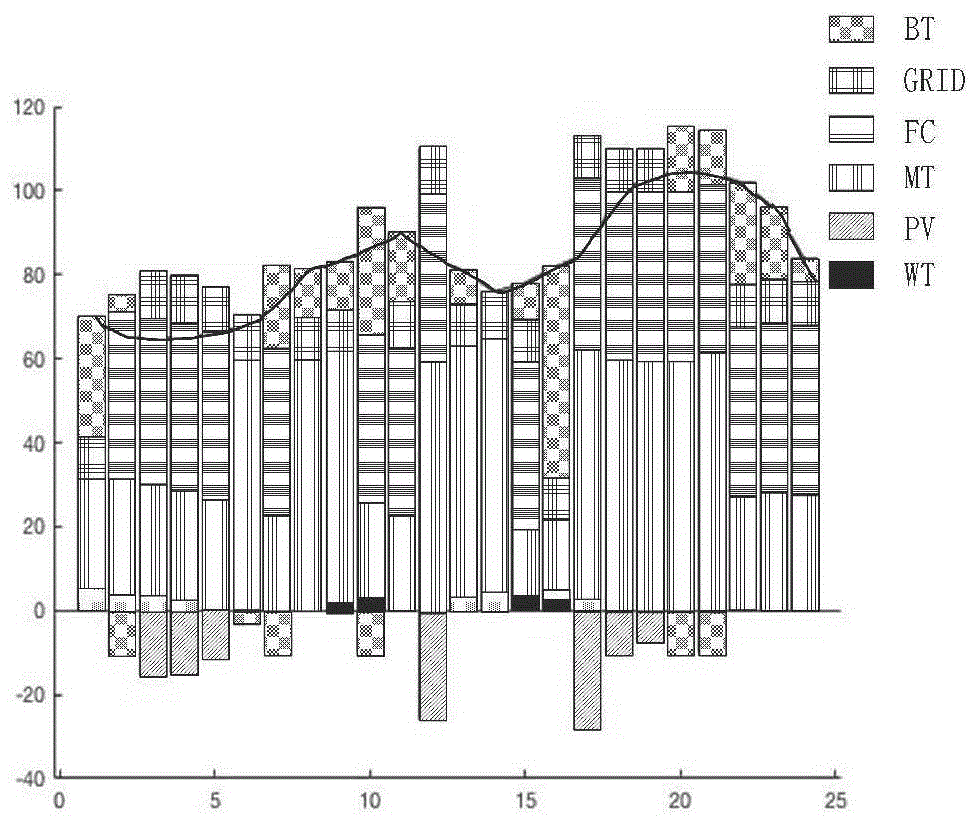
图5是采用策略一，即微电源优先级高于主网，若微电源功率不够，则向主网购电时冬季典型日系统优化结果分析图。

图6是采用策略二，即微电源与主网优先级相同，若微电源电量不够，只能从主网购电时冬季典型日系统优化结果分析图。

图7是采用策略三，微电源与主网优先级相同，若微电源电量不足，不限制从主网购电时冬季典型日系统优化结果分析图。

具体实施方式

下面结合附图和具体实施方式对本发明进行详细说明，但本发明并不限于这些方式。

本发明基于鹦鹉算法的多能源电力系统优化调度的方法，步骤为：

步骤1、建立考虑经济性和环保性的多能源电力系统优化调度的数学模型；

步骤2、设计鹦鹉算法；

步骤3、构建三种不同的多能源电力系统优化调度策略，对鹦鹉算法的有效性进行验证。

其中步骤1具体为：

本发明主要针对5种类型的发电单元发电系统进行了分析，分析其基本工作原理与特点、功率输出与成本建模等几个主要方面，为多能源环境下电力系统的优化以及调度系统分析设计做准备。

步骤1.1，构建包含光伏发电单元、风力发电单元、微型燃气轮机、燃料电池、储能单元的多能源电力系统各个发电单元的输出特性和成本组成：

1)光伏发电单元(Photovoltaic cell,PV)：

光电的主要特性如下所示：

式中，Kr＝0.0017(A/℃)，Tr＝301.18K，其中P是光伏板发出的功率，V是光伏板发出的电压，I是光伏板发出的电流，m是并联板电池数，Iph是光伏组件经由光照射所产生，I0是初始电流，q是电池内部电子电量常量，Rs是串联单向电阻，n是串联电池数，A是二极管特性拟合系数，Kr是玻尔兹曼常数，Tr是标准温度，T是测量时刻的温度。

在实际应用时，由于系统出力受光伏电池环境温度和太阳辐射下系统强度的多种因素影响，所以会以标准条件下来修正：

式中：GSTC＝1000W/m2，k＝-0.47％/℃，Tr＝25℃，GSTC是标准太阳辐照强度，GING是实际太阳辐照强度k是功率温度系数，Tc是实际温度，Tr是标准温度。

太阳能光伏燃料电池直接从太阳获取的能量，属于可再生能源，还应该全方位考量其工作费用和维修费用。

2)风力发电单元(Wind Turbine generator,WT)：

风电的功率特性如下：

在实际条件下，此处不考虑环保成本与利用率成本，只考虑其修理的成本，其中V是风机输入的风速，Vr是标准风速，Pr是标准功率，PWT是风机输出功率，Vco是风机切出风速，Vci是风机切入风速。

3)微型燃气轮机(Micro gas Turbine,MT)：

微型燃气轮机功率函数模型如下：

式中，ηMT表示燃气轮机工作效率，PMT表示燃气轮机功率。

微型通用燃气轮机的正常维护运行以及日常维护费用成本相关函数：

式中，KOMMT表示燃气轮机单位进修价格，这里直接取0.047元/kWh，其中，KOMMT是微型通用燃气轮机的正常维护运行以及日常维护费用成本系数，COMMT是微型通用燃气轮机的正常维护运行以及日常维护费用成本。

微型燃汽轮机的外部污染治理排放系数及其治理费用和成本的函数计算如下式所示：

其中，CEMMT是微型燃汽轮机的外部污染治理排放系数及其治理费用和成本，λk是排放因子，αk是折扣系数。

4)燃料电池(Fuel Cell,FC)：

P为40kW，其功率输出PFC与发电效率ηFC的关系可由下式表示：

ηFC＝-0.0023PFC+0.6735 (7)

其中，ηFC是燃料电池的效率；

在维持燃料电池发电动力系统正常稳态持续发电的过程中，燃料电池的有效输入量和燃料电池输出能耗投入的发电成本的比例关系用下式进行表示：

式中：LHVng是天然气低热值取9.7kWh/m3，Cng是天然气成本，PFC(t)是t时刻燃料电池的功率，CFFC(t)是t时刻燃料电池费用，ηFC(t)是燃料电池效率。

燃料转化电池的正常工作运行以及维护管理成本可用下式来表示：

其中，CEMFC是燃料转化电池的正常工作运行以及维护管理成本，αk是折扣系数，λk是排放因子。

5)储能单元(BatteryTurbine,BT)：

本文充分考虑了多能源电力蓄电池的两种重要约束，即蓄电池充放电功率约束和蓄电池最大容量约束，所以便于蓄电池的应用在t时刻荷电状态(State OfCharge,SOC)可表示为：

式中，I是蓄电池的电流，PBT是蓄电池的功率，UBT是蓄电池的电压，SOC是蓄电池的荷电状态，σsdr是蓄电池的自放电率，ηbce是蓄电池的充放电效率，C是蓄电池的电池容量，Δt是时间间隔，取Δt＝1h,ηbce放电时其值为1，充电时一般在0.65～0.85范围内。

步骤1.2，构建多能源电力系统环保经济运行的目标函数：

步骤1.2.1，多目标分析：

为更好地使多能源电力系统的优化和节约运行，应当研究设置多能源电力系统优化经济调度的基本数学模型，该数学模型有目标约束条件以及基本目标函数这两个主要组成部分。在这之中，多能源优化型电力系统需要优化经济调度的主要基本目标有：(1)污染治理成本最小；(2)各微电源机组出力、蓄电池的剩余容量、系统与主网交互能量在限制范围内；(3)与主网交易成本最小；(4)运行维护成本最小；(5)系统中冷热电负荷的平衡情况；(6)微电源燃料成本最少。

步骤1.2.2，确定目标函数：

1)经济成本目标函数

多能源电力系统可获得的利益很大，也可以说每个单元有最小的操作成本，这一操作成本包括微电网与主网交互成本、运行维护成本、制热收益、孤网负荷补偿成本、制冷收益以及微电源的燃料成本。

式中，C1是运行成本，Cf是燃料成本，COM是检修维护成本，Cgeid是微网主网交互成本，Csh是制热成本，Csc是制冷成本，CL是补偿成本，e、b是费用考虑系数，当这两个值取e＝1,b＝0时，系统并网工作，主网与系统之间存在交互成本；e＝0,b＝1，即系统孤网工作，要取掉一定比例的负荷，那么这种情况下就有切负荷补偿成本。

其中：

Cgrid(t)＝Cg(t)Pg(t)-Cs(t)Ps(t) (15)

Csh(t)＝Qho×Kho (16)

Csc(t)＝Qco×Kco (17)

CL(t)＝Cbu×PCL(t) (18)

其中，LHVng是天然气低热值取9.7kWh/m3，Cng是天然气成本，PFC(t)是t时刻燃料电池的功率，CFFC(t)是t时刻燃料电池费用，ηFC(t)是燃料电池效率；Pi是第i个发电单元的输出功率，ηi第i个发电单元的效率，COM是检修维护成本，KOMi是第i个发电单元正常维护运行以及日常维护费用成本系数，Cgrid是微网主网交互成本，Cg是微网向主网购电成本，Pg是微网向主网购电功率，Cs是微网向主网卖电成本，Ps是微网向主网卖电功率，Csh是制热成本，Qho是热值量，Kho是制热系数，Csc是制冷成本，Qco是冷值量，Kco制冷系数，CL是补偿成本，Cbu是微网支付的停电电量损失，PCL切负荷功率，n是发电单元总数，i是发电单元编号；

2)环保目标函数

这一目标函数是考虑到多能源电力系统的环境效益最大，即能源的污染排放和治理的成本最小，表示公式如下：

式中：C2是环保成本，CK处理污染物惩罚系数，rik第k类型排放的i个发电单元的输出功率系数，Pi是第i个发电单元的输出功率，α是外部折扣系数，rgridk是第k类型排放的微网主网交互系数，Cg是微网向主网购电成本，P是微网向主网购电功率，t是调度的时间，T是调度的总时间，M是排放类型(NOX、SO2或者CO2)数，k是排放类型，n是发电单元总数，i是发电单元编号；

步骤1.2.3，构建多能源电力系统环保经济运行的约束条件：

在掌握正确建立多通道能源系统优化控制和调度的优化控制目标函数的基础上，应当全方位理解多能源系统中多种控制和约束的条件，更全面的各种约束控制条件形成方式如下所述：

1)电功率平衡约束

其中，Pi是第i个发电单元发出的功率，Pball是蓄电池释放的功率，Pgrid是微网主网交互功率，PL是孤网下切负荷功率，β是运行系数，PCL是切负荷功率，当系统并网运行时，β＝0；当系统孤网运行时，β＝1；

2)冷热平衡约束

多能源电力系统中冷热电联供系统需要满足用户需求，它能使用下面这一公式理解：

其中，Qho是制热量，是第k个冷热电联供系统制热量，Qco是制冷量，是第k个冷热电联供系统制冷量，是冷热电联供系统制热量最大值，是冷热电联供系统制热量最小值，是冷热电联供系统制冷量最大值，是冷热电联供系统制冷量最小值；M是冷热电联供系统的总数；

3)微源功率的限定值的约束

其中，和分别表示发电单元发出功率的最大值和最小值。

4)蓄电池运行约束

其中，Sin为输入荷电状态，SOCmin为最小荷电状态，SOCmax为最大荷电状态，Pball为蓄电池的充放电功率，为蓄电池最小的充放电功率，为蓄电池最大的充放电功率。

5)多能源电力系统与主网允许传输功率约束

其中，和分别表示电网传输功率的最大值和最小值。

所述的步骤2，设计鹦鹉算法的具体步骤为：

在建立了数学优化调度模型后，模型的经济性求解问题就成为了解决优化调度问题的重要关键。针对复杂的模型优化调度问题的解决这种非线性动力系统，近些年大量采取的是传统的PSO算法。虽然传统的PSO有诸多优点，但也同时存在一些技术缺陷，其迭代非线性容易陷入局部最优，易产生发散，收敛和低精度的缺点。受到鹦鹉具有自我学习能力与不同环境适应能力的启发，对于上面PSO的缺点，利用自适应权重法以及引入非线性收缩精度等学习因子两种措施来解决，最终生成的算法本发明称之为鹦鹉算法；

步骤2.1引入自适应权重法

由描述可知，权重公式描述了鹦鹉个体上一代运动速度对当前一代的运动速度的一个线性周期变化率的影响。w的统计取样数值区间大小直接地会影响着w和PSO两个局部算法寻优的计算能力。通常这种状态下，取到w的越高，全局寻优的计算强度也越高，在这期间局部寻优的计算强度越低；而当w越低时，结果则正好相反。依据以上计算方法的应用特征，本文以非线性运动法作为计算物体惯性运动权重w的基本方法和应用策略。其需要改进的计算公式如下：

式中，wmax、wmin分别表示为最大权重值和最小权重值，一般取wmin＝4.0，wmax＝9.0；惯性权重和适应系数的最小值会随着自适应鹦鹉个体的目标适应度函数值的大小改变而发生改变，所以该惯性权重又命名为自适应权重；

步骤2.2引入学习因子

在鹦鹉算法优化进程中，两异步速度变化的群算法学习因子c1、c2会随着优化时间的长短发生不同的改变。通过对需要学习的因子进行适当的动态调整，不仅可以有利于其群算法收敛到快速的全局最优解，而且同时还可以大大加快鹦鹉算法的收敛速度。因此对于鹦鹉个体优化作出以下的要求：在鹦鹉个体的群算法开始和结束阶段，鹦鹉个体必须具有较强的自我参与学习的能力，应该需要加强其鹦鹉个体的全局学习和搜索的能力；而在鹦鹉算法寻优的快速开始和结束时，鹦鹉个体必须具有较弱的自我参与社会学习的能力和较强的自我社会学习的能力，因此可以加快其算法收敛的速度，有利于快速的算法收敛得到快速的全局最优解，着力于这两个需要学习的因子分别对其做出适当的学习和动态模拟优化，其动态优化如下：

式中：c1是第1个学习因子，c1f是第1个最终学习因子，c1t是第1个初始学习因子，tmax是最大时间，t是时间，c2是第2个学习因子，c2f是第2个最终学习因子，c2t是第2个初始学习因子。取c1t＝c1f＝2.5，c1t＝c1f＝0.5。

所述步骤3，构建三种不同的多能源电力系统优化调度策略，对鹦鹉算法的有效性进行验证的具体步骤为：

步骤3.1，多能源电力系统的多目标函数处理方法：

1)在通常情况下，多目标系统优化的计算方法和基本模型：

式中：f(X)是总目标函数，f1(X),f2(X),…,fm(X)是m个不同的子目标函数，m表示个数的多少，gi(X)为不等式约束，i表示等式约束的个数，hj(X)表示等式约束，j表示等式约束的个数，X为n个变量x1,x2,…,xn所组成的n维决策变量。在多目标优化问题中，取不等式约束m≥2；等式约束取s.t.gi(X)≥0和hj(X)＝0；

2)多能源电力系统的多目标函数处理办法：

多目标优化的各个子目标较难同时实现总目标最优化，因此采用一种线性加权函数求和法对多目标进行了最优化，来实现多目标电力系统的优化，具体可以表示为：

minf(X)＝w1f1(X)+w2f2(X) (31)

式中：f(X)为总的目标函数，f1(X)为第1个目标函数，f2(X)为第2个目标函数，w1，w2分别表示第1个目标函数和第2个目标函数的权重。w1≥0,w2≥0，且满足w1+w2＝1，随机权重w1和w2由下式确定：

随机权重w1和w2由下式确定：

式中，ri是非负随机数，r1，r2是均是非负随机数；

步骤3.2，多能源电力系统的约束条件处理方法：

利用罚函数法处理约束条件，它将优化问题中含有不等式约束和等式约束的函数经过加权优化处理后，与原优化目标函数相结合，可以直接得到一个新的目标函数，此时，原约束问题转化成新的无约束条件的优化问题，对这个无约束的优化问题进行求解即可。

步骤3.3，构建三种不同的多能源电力系统优化调度策略：

在对该类系统进行设计，及对能源进行调度时使用的管理策略进行优化时，除了会受到其内部的具体结构的影响，也跟电力资源市场中所推行的相关解决方案存在显著关联。根据多能电力系统是否与主网之间的并网协同运行，确定微电源和主网的优先级，构建了以下管控策略：

策略一：微电源优先级高于主网，若微电源功率不够，则向主网购电；

策略二：微电源与主网优先级相同，若微电源电量不够，只能从主网购电；

策略三：微电源与主网优先级相同，若微电源电量不足，不限制从主网购电；

步骤3.4，采用鹦鹉算法求解三种不同的多能源电力系统优化管控策略：

在对多能源电力系统的优化管控的数学模型中的每个变量的异同点做出有效解释后，这一算法的步骤可以概括如下：

首先，生成随机移动的鹦鹉种群，初始化全部随机移动鹦鹉个体的初始值和鹦鹉个体的移动速度v，并且随机设定鹦鹉个体移动位置以及各种移动参数；

其次，评价每个鹦鹉个体的适应度，计算个体极值Pbest及全局极值gbest，并根据相关公式对被测鹦鹉个体的移动区域和移动速度v的两个参数进行更新；

再次，对学习习惯性的权重因子进行调整，并通过比较迭代后鹦鹉个体的适应度值的大小与上一次迭代后鹦鹉个体的适应度值的大小，来决定是否要更新个体极值和全局极值；

最后，根据是否达到迭代的次数或者最大适应参数值没有发生变化两个条件来判断是否终止算法，若满足条件之一，则算法结束，若不满足，则重新进行初始化进行相关操作。具体的求解流程图如图1所示。

实施例

在这一部分中，将在冬、夏季典型日时基于该系统给某农村区域供电当做这次探究的案例，涉及的数据主要为冬季、夏季电冷热负荷曲线典型日的光伏发电功率、风电功率预测曲线、微电源性能参数、冬夏季MT出力曲线。

1)不同目标权重系数下的仿真结果分析

在这一节的内容中，采用策略三。将冬季工作日的相关数据中包含的热负荷的情况当做计算案例，利用鹦鹉算法对系统在能量方面的调度情况进行优化，且不用对冬季典型日中在热负荷方面的情况进行考虑。w1,w2代表的是系统在运行时付出的成本及对排放的污染物进行治理方需要付出成本对应的权重系数，二者对应的数值不同，最终得到的结果也会存在差别。图2、3、4为冬季典型日时不同w1,w2情况下的仿真结果，图中黑色折线为电负荷出力曲线。

当对发电成本进行计算时确定的权重系数存在区别时，冬季典型日对应的成本优化的具体情况列示在表1中：

表1不同权重系冬季典型日系统的成本比较(单位：元)

从表1各不同权重系数下成本的比较可知：多能电力系统的优化调度与系统目标函数的权重大小有关。仿真得到的结果显示，系统运行成本在相应权重减小的情况下出现提升的情况，而治理费用会在相应权重增加的情况下得到降低。

2)不同运行策略下的仿真结果分析

本节将对多能电力系统经济及环境方面的效益进行了综合考虑，处于冬季典型日时，以三种不同的运行策略来进行发电，图5、6、7为对应的功率及输出的具体情况。

基于上述三种策略，系统在冬季典型日运行时，对应的成本的具体情况列示在表2中。

表2不同从策略下冬季典型日的成本比较(单位：元)

从表2各运行策略下成本的比较可知多能电力系统优化调度与运行策略有关。

本发明最终仿真结果与结论保持一致，并且利用鹦鹉算法，得出的曲线并未像其他算法出现收敛性差、容易陷入局部最优等问题。这代表这次探究中构建的相关模型及使用的鹦鹉算法，具有较好的可行性，相关的结果也是较好的。